题目内容
【题目】解关于![]() 的不等式
的不等式![]() .
.
【答案】当![]() 时,解集为:R ;当
时,解集为:R ;当![]() 时,解集为:
时,解集为:![]() ;当
;当![]() 时,解集为
时,解集为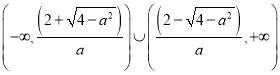 ;当
;当![]() 时,解集为
时,解集为![]() ; 当
; 当![]() 时,解集为
时,解集为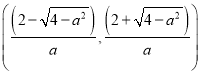 ;当
;当![]() 时,不等式的解集为:
时,不等式的解集为:![]() .
.
【解析】
对参数![]() 展开讨论,从而求解不等式.
展开讨论,从而求解不等式.
(1)当![]() 时,原不等式等价于
时,原不等式等价于![]() ,
,
解得![]() ,故不等式解集为
,故不等式解集为![]() ;
;
(2)当![]() 时,原不等式为二次不等式,
时,原不等式为二次不等式,![]() ,
,
①当![]() 时,即
时,即![]() 时,
时,
不等式对应的方程![]() 有两个不相等实根,
有两个不相等实根,
解得: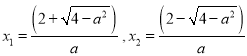
当![]() 时,
时,![]() ,故
,故
不等式的解集为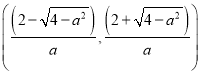 ;
;
当![]() 时,
时,![]() ,故
,故
不等式的解集为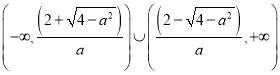
②当![]() 时,即
时,即![]() 时,
时,
不等式对应的方程![]() 有两个相等的实根,
有两个相等的实根,
即![]()
当![]() 时,不等式的解集为:
时,不等式的解集为:![]()
当![]() 时,不等式的解集为:
时,不等式的解集为:![]() .
.
③当![]() 时,即
时,即![]() 时,
时,
不等式对应的方程![]() 没有实数根,故
没有实数根,故
当![]() 时,不等式的解集为:R.
时,不等式的解集为:R.
当![]() 时,不等式的解集为:
时,不等式的解集为:![]() .
.
综上所述: 当![]() 时,解集为:R
时,解集为:R
当![]() 时,解集为:
时,解集为:![]() .
.
当![]() 时,解集为
时,解集为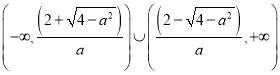
当![]() 时,解集为
时,解集为![]()
当![]() 时,解集为
时,解集为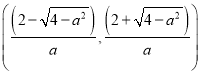
当![]() 时,不等式的解集为:
时,不等式的解集为:![]() .
.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目