Question

【题目】如图，在四棱柱中，侧棱底面，，，，，且点和分别为和的中点

（I）求证：平面；

（II）求二面角的正弦值；

（III）设为棱上的点，若直线和平面所成角的正弦值为，求的长。

Answer 1

【答案】（I）见解析（II）（III）

【解析】

（I）建立空间直角坐标系，通过与面的法向量垂直可证得结果；（II）分别求解出平面和平面的法向量，求解出法向量成角的余弦值，根据同角三角函数关系可得所求正弦值；（III）假设，则与平面法向量的夹角的余弦值的绝对值即为直线和平面所成角的正弦值，从而构造方程求得，继而求得.

（I）以为原点，建立如下图所示的空间直角坐标系：

则，，，

，，，

平面的法向量

又，

，面 面

（II）设面的法向量，且，

，令，则，

设面的法向量，且，

，令，则，

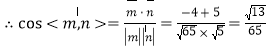
即二面角的正弦值是

（III）设，则

又面的法向量

，解得：或（舍）

，即