题目内容
已知直线的倾斜角为α,且 ,则该直线的斜率为________
,则该直线的斜率为________
-7
分析:根据 ,推出
,推出 ,求出
,求出 ,然后解出sinα、cosα的值,从而求出直线的斜率.
,然后解出sinα、cosα的值,从而求出直线的斜率.
解答:直线的倾斜角为α,所以该直线的斜率k=tanα,
因为
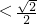 所以
所以 ,
,
可得sinα+cosα=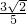 cosα-sinα=-
cosα-sinα=-
所以sinα= cosα=-
cosα=-
所以tanα=-7
故答案为:-7
点评:本题考查最小的斜率,两角和与差的正弦、余弦,三角函数值估计角的范围,是中档题.
分析:根据
 ,推出
,推出 ,求出
,求出 ,然后解出sinα、cosα的值,从而求出直线的斜率.
,然后解出sinα、cosα的值,从而求出直线的斜率.解答:直线的倾斜角为α,所以该直线的斜率k=tanα,
因为

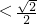 所以
所以 ,
,
可得sinα+cosα=
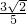 cosα-sinα=-
cosα-sinα=-
所以sinα=
 cosα=-
cosα=-
所以tanα=-7
故答案为:-7
点评:本题考查最小的斜率,两角和与差的正弦、余弦,三角函数值估计角的范围,是中档题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
 的倾斜角为
的倾斜角为 ,下列可以作为直线
,下列可以作为直线 B.
B.
 C.
C.
 D.
D.
