题目内容
若过点(0,0)的直线L与曲线y=x3-3x2+2x相切,则直线L的方程为______.
设直线l:y=kx.∵y′=3x2-6x+2,∴y′|x=0=2,
又∵直线与曲线均过原点,于是直线y=kx与曲线y=x3-3x2+2相切于原点时,k=2.直线L的方程为 2x-y=0
若直线与曲线切于点(x0,y0)(x0≠0),则k=
,∵y0=x03-3x02+2x0,
∴
=x02-3x0+2,
又∵k=y′|_x=x0=3x02-6x0+2,
∴x02-3x0+2=3x02-6x0+2,∴2x02-3x0=0,
∵x0≠0,∴x0=
,∴k=x02-3x0+2=-
,直线L的方程为 x+4y=0
故答案为:2x-y=0或x+4y=0
又∵直线与曲线均过原点,于是直线y=kx与曲线y=x3-3x2+2相切于原点时,k=2.直线L的方程为 2x-y=0
若直线与曲线切于点(x0,y0)(x0≠0),则k=
| y0 |
| x0 |
∴
| y0 |
| x0 |
又∵k=y′|_x=x0=3x02-6x0+2,
∴x02-3x0+2=3x02-6x0+2,∴2x02-3x0=0,
∵x0≠0,∴x0=
| 3 |
| 2 |
| 1 |
| 4 |
故答案为:2x-y=0或x+4y=0

练习册系列答案
相关题目
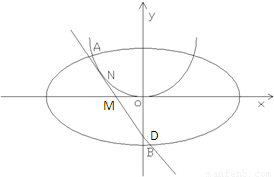
 椭圆E:
椭圆E: 过点A(a,0),B(0,b)的直
过点A(a,0),B(0,b)的直 ,原点到该直线的距离为
,原点到该直线的距离为 .
. 求直线MN的方程;
求直线MN的方程; 交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由。
交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由。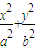 =1(a>b>0)离心率为
=1(a>b>0)离心率为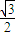 ,且过P(
,且过P(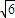 ,
,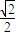 ).
). ,0),且与开口朝上,顶点在原点的抛物线C切于第二象限的一点N,直 线l与椭圆E交于A,B两点,与y轴交与D点,若
,0),且与开口朝上,顶点在原点的抛物线C切于第二象限的一点N,直 线l与椭圆E交于A,B两点,与y轴交与D点,若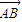 =
=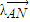 ,
,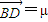
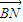 ,且λ+μ=
,且λ+μ= ,求抛物线C的标准方程.
,求抛物线C的标准方程.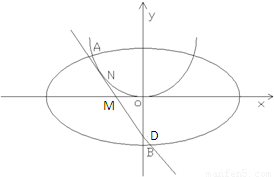
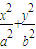 =1(a>b>0)离心率为
=1(a>b>0)离心率为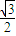 ,且过P(
,且过P(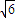 ,
,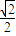 ).
). ,0),且与开口朝上,顶点在原点的抛物线C切于第二象限的一点N,直 线l与椭圆E交于A,B两点,与y轴交与D点,若
,0),且与开口朝上,顶点在原点的抛物线C切于第二象限的一点N,直 线l与椭圆E交于A,B两点,与y轴交与D点,若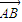 =
=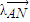 ,
,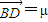
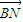 ,且λ+μ=
,且λ+μ= ,求抛物线C的标准方程.
,求抛物线C的标准方程.