题目内容
椭圆E: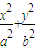 =1(a>b>0)离心率为
=1(a>b>0)离心率为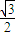 ,且过P(
,且过P(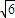 ,
,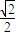 ).
).(1)求椭圆E的方程;
(2)已知直线l过点M(-
 ,0),且与开口朝上,顶点在原点的抛物线C切于第二象限的一点N,直 线l与椭圆E交于A,B两点,与y轴交与D点,若
,0),且与开口朝上,顶点在原点的抛物线C切于第二象限的一点N,直 线l与椭圆E交于A,B两点,与y轴交与D点,若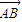 =
=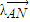 ,
,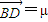
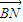 ,且λ+μ=
,且λ+μ= ,求抛物线C的标准方程.
,求抛物线C的标准方程.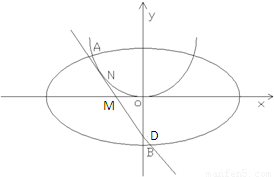
【答案】分析:(1)利用离心率计算公式、点在椭圆上及a,b,c的关系可得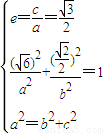 ,解出即可;
,解出即可;
(2)设抛物线C的方程为y=ax2(a>0),直线与抛物线C切点为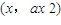 .利用导数的几何意义可得切线的斜率,进而得到切线方程,即可得到切点N,进一步简化切线方程,把直线l的方程与椭圆的方程联立得到根与系数的关系,再利用已知向量关系式
.利用导数的几何意义可得切线的斜率,进而得到切线方程,即可得到切点N,进一步简化切线方程,把直线l的方程与椭圆的方程联立得到根与系数的关系,再利用已知向量关系式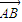 =
=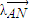 ,
,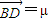
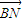 ,且λ+μ=
,且λ+μ= ,即可得到a及抛物线C的标准方程.
,即可得到a及抛物线C的标准方程.
解答:解.(1)由题意可得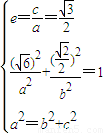 ,解得
,解得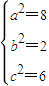 ,
,
∴椭圆E的方程为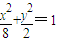 .
.
(2)设抛物线C的方程为y=ax2(a>0),
直线与抛物线C切点为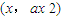 .
.
∵y′=2ax,∴切线l的斜率为2ax,
∴切线方程为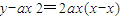 ,
,
∵直线l过点M ,∴
,∴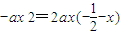 ,
,
∵点N在第二象限,∴x<0,
解得x=-1.∴N(-1,a).
∴直线l的方程为y=-2ax-a.
代入椭圆方程并整理得:代入椭圆方程整理为(1+16a2)x2+16a2x+4a2-8=0.
设A(x1,y1),B(x2,y2).
∴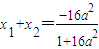 ,
,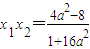 .
.
由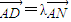 ,
,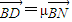 ,
,
∴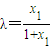 ,
,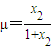 .
.
∴λ+μ=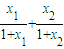 =
=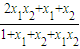 =
= .
.
∵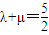 ,∴
,∴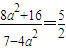 ,又a>0,解得
,又a>0,解得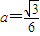 .
.
∴抛物线C的标准方程为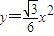 ,其标准方程为
,其标准方程为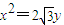 .
.
点评:本题综合考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为根与系数的关系、直线与抛物线相切问题、导数的几何意义、向量的运算等基础知识与基本技能,考查了推理能力和计算能力.
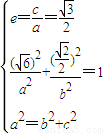 ,解出即可;
,解出即可;(2)设抛物线C的方程为y=ax2(a>0),直线与抛物线C切点为
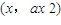 .利用导数的几何意义可得切线的斜率,进而得到切线方程,即可得到切点N,进一步简化切线方程,把直线l的方程与椭圆的方程联立得到根与系数的关系,再利用已知向量关系式
.利用导数的几何意义可得切线的斜率,进而得到切线方程,即可得到切点N,进一步简化切线方程,把直线l的方程与椭圆的方程联立得到根与系数的关系,再利用已知向量关系式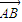 =
=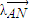 ,
,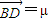
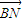 ,且λ+μ=
,且λ+μ= ,即可得到a及抛物线C的标准方程.
,即可得到a及抛物线C的标准方程.解答:解.(1)由题意可得
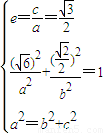 ,解得
,解得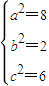 ,
,∴椭圆E的方程为
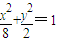 .
.(2)设抛物线C的方程为y=ax2(a>0),
直线与抛物线C切点为
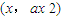 .
.∵y′=2ax,∴切线l的斜率为2ax,
∴切线方程为
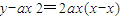 ,
,∵直线l过点M
 ,∴
,∴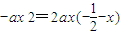 ,
,∵点N在第二象限,∴x<0,
解得x=-1.∴N(-1,a).
∴直线l的方程为y=-2ax-a.
代入椭圆方程并整理得:代入椭圆方程整理为(1+16a2)x2+16a2x+4a2-8=0.
设A(x1,y1),B(x2,y2).
∴
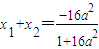 ,
,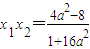 .
.由
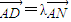 ,
,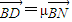 ,
,∴
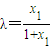 ,
,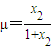 .
.∴λ+μ=
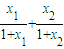 =
=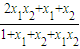 =
= .
.∵
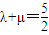 ,∴
,∴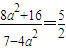 ,又a>0,解得
,又a>0,解得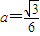 .
.∴抛物线C的标准方程为
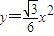 ,其标准方程为
,其标准方程为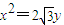 .
.点评:本题综合考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为根与系数的关系、直线与抛物线相切问题、导数的几何意义、向量的运算等基础知识与基本技能,考查了推理能力和计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

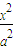 +
+ =1(a>b>0)的右焦点,点M在椭圆E上,以M为圆心的圆与x轴切于点F,与y轴交于A、B两点,且△ABM是边长为2的正三角形;又椭圆E上的P、Q两点关于直线l:y=x+n对称.
=1(a>b>0)的右焦点,点M在椭圆E上,以M为圆心的圆与x轴切于点F,与y轴交于A、B两点,且△ABM是边长为2的正三角形;又椭圆E上的P、Q两点关于直线l:y=x+n对称.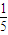 )时,求直线PQ的方程;
)时,求直线PQ的方程;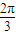 ,求△PCQ面积的最大值.
,求△PCQ面积的最大值.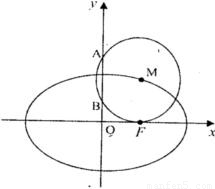
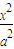 +
+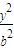 =1(a>b>0)的右焦点,点M在椭圆E上,以M为圆心的圆与x轴切于点F,与y轴交于A、B两点,且△ABM是边长为2的正三角形;又椭圆E上的P、Q两点关于直线l:y=x+n对称.
=1(a>b>0)的右焦点,点M在椭圆E上,以M为圆心的圆与x轴切于点F,与y轴交于A、B两点,且△ABM是边长为2的正三角形;又椭圆E上的P、Q两点关于直线l:y=x+n对称.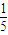 )时,求直线PQ的方程;
)时,求直线PQ的方程;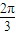 ,求△PCQ面积的最大值.
,求△PCQ面积的最大值.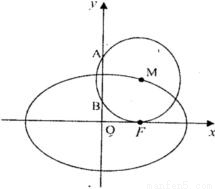
 =1(a>b>o)的离心率e=
=1(a>b>o)的离心率e= ,且经过点(
,且经过点( ,1),O为坐标原点。
,1),O为坐标原点。
 =1(a>b>o)的离心率e=
=1(a>b>o)的离心率e= ,且经过点(
,且经过点( ,1),O为坐标原点。
,1),O为坐标原点。