题目内容
7.已知O为△ABC的外心,若AC=1,$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,且x+2y=1,则$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\frac{1}{2}$.分析 由题意画出图形,再由已知向量等式求出$\overrightarrow{AB}$,代入$\overrightarrow{AB}$•$\overrightarrow{AC}$展开,结合向量在向量方向上投影的概念求解.
解答 解:如图,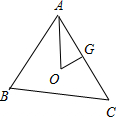
由$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,得$x\overrightarrow{AB}=\overrightarrow{AO}-y\overrightarrow{AC}$,
∴$\overrightarrow{AB}=\frac{\overrightarrow{AO}-y\overrightarrow{AC}}{x}$,
则$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\frac{1}{x}(\overrightarrow{AO}-y\overrightarrow{AC})•\overrightarrow{AC}$=$\frac{1}{x}\overrightarrow{AO}•\overrightarrow{AC}-\frac{y}{x}|\overrightarrow{AC}{|}^{2}$
=$\frac{1}{x}(\frac{1}{2}|\overrightarrow{AC}{|}^{2}-y|\overrightarrow{AC}{|}^{2})=\frac{1}{x}(\frac{1}{2}-y)=\frac{1-2y}{2x}=\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查平面向量的数量积运算,考查向量在向量方向上投影的概念,考查了推理能力与计算能力,属于中档题.

 出彩同步大试卷系列答案
出彩同步大试卷系列答案| A. | (-∞,-2] | B. | (2,3] | C. | [3,+∞) | D. | [-2,3] |
| A. | $\sqrt{5}$ | B. | 5 | C. | 2$\sqrt{5}$ | D. | 10 |
| A. | x=kπ+$\frac{π}{2}$,k∈Z | B. | x=$\frac{kπ}{2}$+$\frac{π}{4}$,k∈Z | C. | x=2kπ+π,k∈Z | D. | x=kπ+$\frac{π}{4}$,k∈Z |
 如图,在四棱锥C-ABCD中,CO⊥平面ABOD,AB∥OD,OB⊥OD,且AB=2OD=12,AD=6$\sqrt{2}$,异面直线CD与AB所成角为30°,点O,B,C,D都在同一个球面上,则该球的半径为( )
如图,在四棱锥C-ABCD中,CO⊥平面ABOD,AB∥OD,OB⊥OD,且AB=2OD=12,AD=6$\sqrt{2}$,异面直线CD与AB所成角为30°,点O,B,C,D都在同一个球面上,则该球的半径为( )| A. | 3$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | $\sqrt{21}$ | D. | $\sqrt{42}$ |