题目内容
解方程：log3(x2-3)=1+log3(x-
)．
| 5 |
| 3 |
考点：对数的运算性质
专题：函数的性质及应用
分析：由原方程可化简得log3(x2-3)=log33(x-
)，利用对数函数的单调性和定义域可得
，解得即可．
| 5 |
| 3 |
|
解答：
解：由原方程化简得log3(x2-3)=log33(x-
)，
∴
，
解得x=2．
经检验x=2是原方程的实数根．
∴原方程的实数根是x=2．
| 5 |
| 3 |
∴
|
解得x=2．
经检验x=2是原方程的实数根．
∴原方程的实数根是x=2．
点评：本题考查了对数函数的单调性和定义域，属于基础题．
练习册系列答案
相关题目
已知a，b∈R且a＞b，则下列不等式中成立的是（ ）
A、
| ||
| B、a2＞b2 | ||
| C、ln（a-b）＞0 | ||
| D、2a-b＞1 |
已知某个几何体的三视图如图所示，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是（ ）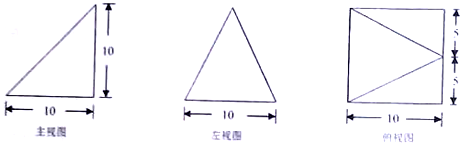
A、
| ||
B、
| ||
| C、1000cm3 | ||
| D、2000cm3 |