题目内容
数列{an}满足:a1=2,an=1
2
解析:![]() sin[
sin[![]() n-
n-![]() ]+
]+![]() (k∈N)
(k∈N)
(注意:答案不唯一,如写成an=![]() sin(
sin(![]() n-
n-![]() )+
)+![]() 即可)
即可)
∵an=1![]() ,又a1=2,∴a2=
,又a1=2,∴a2=![]() ,a3=-1,a4=2.故T=3,即
,a3=-1,a4=2.故T=3,即![]() =3.∴ω=
=3.∴ω=![]() ,an=Asin(
,an=Asin(![]() n+φ)+B.
n+φ)+B.
把a1=2,a2=![]() ,a3=-1代入,得
,a3=-1代入,得
①-②,得Acosφ=![]() .④
.④
②-③,得A(![]() cosφ-
cosφ-![]() sinφ)=
sinφ)=![]() .⑤
.⑤
④÷⑤,得tanφ=-![]() .∵|φ|<
.∵|φ|<![]() ,∴φ=-
,∴φ=-![]() .代入④得A=
.代入④得A=![]() .再代入③得B=
.再代入③得B=![]() .
.
故此通项公式可以为an=![]() sin(
sin(![]() n-
n-![]() )+
)+![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
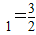 ,a
,a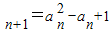 (n∈N*),则m=
(n∈N*),则m=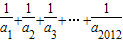 的整数部分是( )
的整数部分是( ) ,那么正数m的最小取值是( )
,那么正数m的最小取值是( )
