题目内容
(10分)已知函数 ,设
,设 为
为 的导数,
的导数,
(1)求 的值;
的值;
(2)证明:对任意 ,等式
,等式 都成立.
都成立.
 ,设
,设 为
为 的导数,
的导数,
(1)求
 的值;
的值;(2)证明:对任意
 ,等式
,等式 都成立.
都成立.(1) ;(2)证明见解析.
;(2)证明见解析.
 ;(2)证明见解析.
;(2)证明见解析.试题分析:(1)本题首先考查复合函数的求导,如
 ;
;(2)要找到式子
 的规律,当然主要是找式子
的规律,当然主要是找式子 的规律,为了达到此目标,我们让
的规律,为了达到此目标,我们让 看看有什么特点,由(1)
看看有什么特点,由(1) ,对这个式子两边求导可得
,对这个式子两边求导可得 ,再求导
,再求导 ,由引可归纳出
,由引可归纳出
 ,从上面过程还可看出应该用数学归纳法证明这个结论.
,从上面过程还可看出应该用数学归纳法证明这个结论.试题解析:(1)由已知
 ,
, ,
,所以
 ,
, ,
,故

 .
.(2)由(1)得
 ,
,两边求导可得
 ,
,类似可得
 ,
,下面我们用数学归纳法证明
 对一切
对一切 都成立,
都成立,(1)
 时命题已经成立,
时命题已经成立,(2)假设
 时,命题成立,即
时,命题成立,即 ,
,对此式两边求导可得

 ,
,即
 ,因此
,因此 时命题也成立.
时命题也成立.综合(1)(2)等式
 对一切
对一切 都成立.
都成立.令
 ,得
,得 ,
,所以
 .
.【考点】复合函数的导数,数学归纳法.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
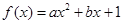 (
(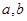 为实数,
为实数,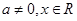 ),
),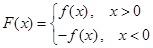 ,⑴若
,⑴若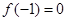 ,且函数
,且函数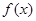 的值域为
的值域为 ,求
,求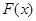 的表达式;
的表达式;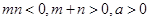 ,且函数
,且函数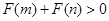 是否大0?
是否大0?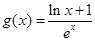 ,当
,当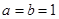 时,证明:对任意实数
时,证明:对任意实数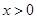 ,
,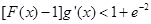 (其中
(其中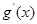 是
是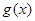 的导函数) .
的导函数) .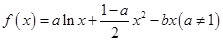 ,曲线
,曲线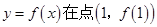 处的切线斜率为0
处的切线斜率为0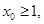 使得
使得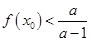 ,求a的取值范围。
,求a的取值范围。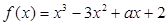 ,曲线
,曲线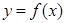 在点
在点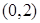 处的切线与
处的切线与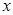 轴交点的横坐标为
轴交点的横坐标为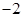 .
.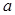 ;
;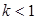 时,曲线
时,曲线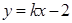 只有一个交点.
只有一个交点.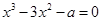 有三个不同的实数解,则a的取值范围是__________.
有三个不同的实数解,则a的取值范围是__________.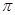 为圆周率,
为圆周率,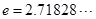 为自然对数的底数.
为自然对数的底数.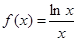 的单调区间;
的单调区间;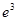 ,
,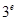 ,
,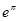 ,
,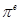 ,
,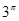 ,
,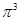 这6个数中的最大数与最小数;
这6个数中的最大数与最小数;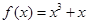 ,
,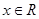 .若当
.若当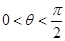 时,不等式
时,不等式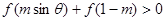 恒成立,则实数
恒成立,则实数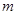 的取值范围是( )
的取值范围是( )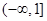
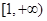
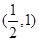
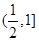
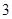 元,并且每件产品需向总公司交
元,并且每件产品需向总公司交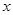 元(
元(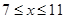 )时,一年的销售量为
)时,一年的销售量为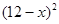 万件.
万件.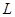 (万元)与每件产品的售价
(万元)与每件产品的售价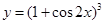 的导数。
的导数。