题目内容
已知函数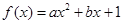 (
(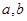 为实数,
为实数,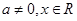 ),
),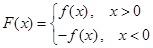 ,⑴若
,⑴若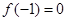 ,且函数
,且函数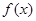 的值域为
的值域为 ,求
,求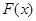 的表达式;
的表达式;
⑵设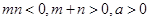 ,且函数
,且函数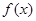 为偶函数,判断
为偶函数,判断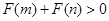 是否大0?
是否大0?
⑶设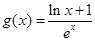 ,当
,当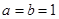 时,证明:对任意实数
时,证明:对任意实数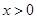 ,
,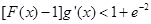 (其中
(其中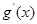 是
是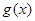 的导函数) .
的导函数) .
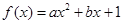 (
(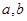 为实数,
为实数,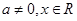 ),
),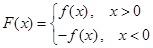 ,⑴若
,⑴若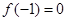 ,且函数
,且函数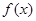 的值域为
的值域为 ,求
,求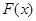 的表达式;
的表达式;⑵设
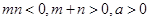 ,且函数
,且函数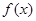 为偶函数,判断
为偶函数,判断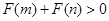 是否大0?
是否大0?⑶设
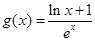 ,当
,当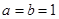 时,证明:对任意实数
时,证明:对任意实数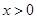 ,
,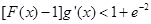 (其中
(其中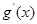 是
是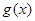 的导函数) .
的导函数) .(1)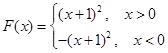 ,(2)
,(2)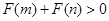 成立,(3)证明略.
成立,(3)证明略.
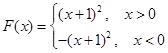 ,(2)
,(2)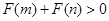 成立,(3)证明略.
成立,(3)证明略.试题分析:(1)由于
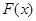 的表达式与
的表达式与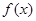 有关,而确定
有关,而确定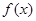 的表达式只需求出待定系数
的表达式只需求出待定系数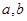 ,因此只要根据题目条件联立关于
,因此只要根据题目条件联立关于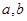 的两个关系即可;(2)由
的两个关系即可;(2)由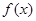 为偶函数可先确定
为偶函数可先确定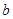 ,而
,而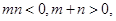 可不妨假设
可不妨假设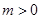 ,则
,则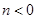 ,代入
,代入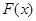 的表达式即可判断
的表达式即可判断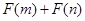 的符号;(3)原不等式证明等价于证明“对任意实数
的符号;(3)原不等式证明等价于证明“对任意实数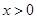 ,
,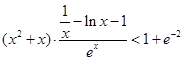 ” 即等价于证明“
” 即等价于证明“ 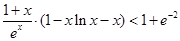 ”,可先证
”,可先证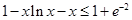 ,再证
,再证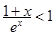 .根据不等式性质,可证得
.根据不等式性质,可证得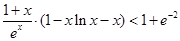 .
.试题解析:⑴因为
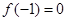 ,所以
,所以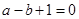 ,因为
,因为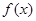 的值域为
的值域为 ,所以
,所以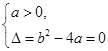 ,所以
,所以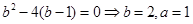 ,所以
,所以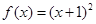 ,所以
,所以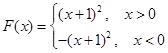 ;
;⑵因为
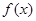 是偶函数,所以
是偶函数,所以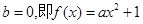 ,又
,又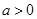 ,所以
,所以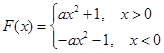 ,因为
,因为 ,不妨设
,不妨设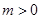 ,则
,则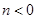 ,又
,又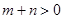 ,所以
,所以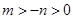 ,此时
,此时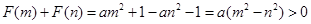 ,所以
,所以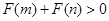 ;
;⑶因为
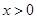 ,所以
,所以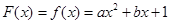 ,又
,又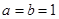 ,则
,则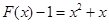 ,因为
,因为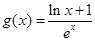 ,所以
,所以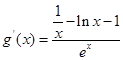 ,则原不等式证明等价于证明“对任意实数
,则原不等式证明等价于证明“对任意实数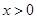 ,
,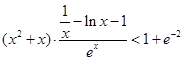 ” 即
” 即 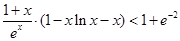 .
.先研究
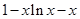 ,再研究
,再研究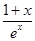 .
.① 记
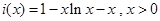 ,
,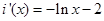 ,令
,令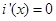 ,得
,得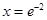 ,当
,当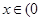 ,
,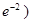 时
时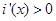 ,
,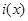 单增;当
单增;当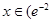 ,
,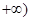 时
时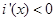 ,
,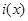 单减. 所以,
单减. 所以,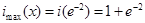 ,即
,即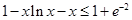 .
.② 记
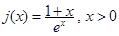 ,
,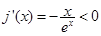 ,所以
,所以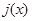 在
在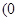 ,
,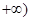 单减,所以,
单减,所以,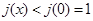 ,即
,即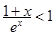 .
.综上①、②知,
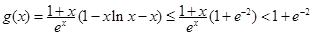 .
.即原不等式得证,对任意实数
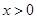 ,
,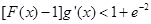 .
.
练习册系列答案
相关题目
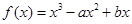 的图象为曲线E.
的图象为曲线E.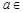 R,函数
R,函数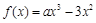 .
.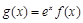 在区间[0,2]上是减函数,求实数a的取值范围.
在区间[0,2]上是减函数,求实数a的取值范围.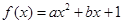 在
在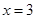 处的切线方程为
处的切线方程为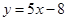 .
.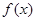 的解析式;
的解析式;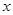 的方程
的方程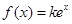 恰有两个不同的实根,求实数
恰有两个不同的实根,求实数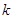 的值;
的值;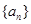 满足
满足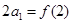 ,
,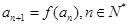 ,求
,求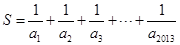 的整数部分.
的整数部分.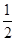 x2+2x+kln x,其中k≠0.
x2+2x+kln x,其中k≠0. ,设
,设 为
为 的导数,
的导数,
 的值;
的值; 都成立.
都成立. 元,每生产一单位产品成本增加
元,每生产一单位产品成本增加 元,已知总收益
元,已知总收益 与年产量
与年产量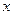 关系是
关系是 ,则总利润最大时,每年生产的产品数量是( )
,则总利润最大时,每年生产的产品数量是( )


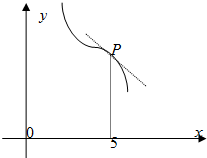
 的导函数
的导函数 的图像如图所示,那么
的图像如图所示,那么
