题目内容
13.已知椭圆W:$\frac{x^2}{4}+{y^2}=1$,过原点O作直线l1交椭圆W于A,B两点,P为椭圆上异于A,B的动点,连接PA,PB,设直线PA,PB的斜率分别为k1,k2(k1,k2≠0),过O作直线PA,PB的平行线l2,l3,分别交椭圆W于C,D和E,F.(Ⅰ)若A,B分别为椭圆W的左、右顶点,是否存在点P,使∠APB=90°?说明理由.
(Ⅱ)求k1•k2的值;
(Ⅲ)求|CD|2+|EF|2的值.
分析 (Ⅰ)不存在点P,使∠APB=90°.理由如下:设P(xP,yP),运用向量垂直的条件和数量积的坐标表示,结合椭圆方程,即可判断;
(Ⅱ)设P(xP,yP),A(xA,yA),运用直线的斜率公式和点差法,化简整理可得所求值;
(Ⅲ)方法一:由于l2,l3分别平行于直线PA,PB,求得直线方程,联立椭圆方程,求得弦长,化简整理,即可得到所求值;
方法二、设C(xC,yC),E(xE,yE),由直线l2,l3都过原点,则D(-xC,-yC),F(-xE,-yE).
由于l2,l3分别平行于直线PA,PB,由平行的条件,求得直线方程,代入椭圆方程,化简整理,即可得到所求值.
解答 解:(Ⅰ)不存在点P,使∠APB=90°.
说明如下:设P(xP,yP).
依题意,此时A(-2,0),B(2,0),
则$\overrightarrow{AP}=({{x_P}+2,{y_P}})$,$\overrightarrow{BP}=({{x_P}-2,{y_P}})$.
若∠APB=90°,则需使$\overrightarrow{AP}•\overrightarrow{BP}=0$,即$x_P^2-4+y_P^2=0$.…(1)
又点P在椭圆W上,所以$\frac{{{x_P}^2}}{4}+{y_P}^2=1$,
把${y_P}^2=1-\frac{{{x_P}^2}}{4}$代入(1)式中解得,xP=±2,且yP=0.
显然与P为椭圆上异于A,B的点矛盾,所以不存在;
(Ⅱ)设P(xP,yP),A(xA,yA),依题意直线l1过原点,则B(-xA,-yA).
由于P为椭圆上异于A,B的点,
则直线PA的斜率${k_1}=\frac{{{y_P}-{y_A}}}{{{x_P}-{x_A}}}$,直线PB的斜率${k_2}=\frac{{{y_P}+{y_A}}}{{{x_P}+{x_A}}}$.
即${k_1}•{k_2}=\frac{y_P^2-y_A^2}{x_P^2-x_A^2}$.
椭圆W的方程化为x2+4y2=4,由于点P和点A都为椭圆W上的点,
则$\left\{\begin{array}{l}x_P^2+4y_P^2=4\\ x_A^2+4y_A^2=4\end{array}\right.$,两式相减得${x_P}^2-{x_A}^2+4({y_P}^2-y_A^2)=0$,
因为点P和点A不重合,所以$1+4×\frac{{{y_P}^2-y_A^2}}{{{x_P}^2-{x_A}^2}}=0$,
即${k_1}•{k_2}=\frac{y_P^2-y_A^2}{x_P^2-x_A^2}=-\frac{1}{4}$;
(Ⅲ)方法一:由于l2,l3分别平行于直线PA,PB,
则直线l2的斜率kCD=k1,直线l3的斜率kEF=k2.
设直线l2的方程为y=k1x,代入到椭圆方程中,
得${x^2}+4k_1^2{x^2}=4$,解得${x^2}=\frac{4}{4k_1^2+1}$.
设C(xC,yC),由直线l2过原点,则D(-xC,-yC).
则${|{CD}|^2}={[{{x_C}-(-{x_C})}]^2}+{[{{y_C}-(-{y_C})}]^2}$=$4(x_C^2+y_C^2)$.
由于yC=k1xC,所以|CD|2=$4(1+k_1^2)x_C^2$,即|CD|2=$16\frac{k_1^2+1}{4k_1^2+1}$.
直线l3的方程为y=k2x,代入到椭圆方程中,
得${x^2}+4k_2^2{x^2}=4$,解得${x^2}=\frac{4}{4k_2^2+1}$.
同理可得${|{EF}|^2}=16\frac{k_2^2+1}{4k_2^2+1}$.
则|CD|2+|EF|2=$16(\frac{k_1^2+1}{4k_1^2+1}+\frac{k_2^2+1}{4k_2^2+1})$.
由(Ⅱ)问${k_1}•{k_2}=-\frac{1}{4}$,且k1≠0,则${k_2}=-\frac{1}{{4{k_1}}}$.
即|CD|2+|EF|2=16$({\frac{k_1^2+1}{4k_1^2+1}+\frac{{\frac{1}{16k_1^2}+1}}{{4\frac{1}{16k_1^2}+1}}})$
化简得|CD|2+|EF|2=16$[{\frac{4k_1^2+4+16k_1^2+1}{4(4k_1^2+1)}}]$.
即|CD|2+|EF|2=20.
方法二:设C(xC,yC),E(xE,yE),
由直线l2,l3都过原点,则D(-xC,-yC),F(-xE,-yE).
由于l2,l3分别平行于直线PA,PB,
则直线l2的斜率kCD=k1,直线l3的斜率kEF=k2,
由(Ⅱ)得${k_1}•{k_2}=-\frac{1}{4}$,可得${k_{CD}}•{k_{EF}}=-\frac{1}{4}$.
由于kCD=k1≠0,则${k_{EF}}=-\frac{1}{{4{k_1}}}$.
由于点C不可能在x轴上,即yC≠0,所以${k_{EF}}=-\frac{x_C}{{4{y_C}}}$,
过原点的直线l3的方程为$y=-\frac{x_C}{{4{y_C}}}x$,代入椭圆W的方程中,
得${x^2}+(4×\frac{1}{16}×\frac{x_C^2}{y_C^2}){x^2}=4$,化简得${x^2}=\frac{16y_C^2}{4y_C^2+x_C^2}$.
由于点C(xC,yC)在椭圆W上,所以$x_C^2+4y_C^2=4$,
所以${x^2}=4y_C^2$,不妨设xE=2yC,代入到直线$y=-\frac{x_C}{{4{y_C}}}x$中,
得${y_E}=-\frac{1}{2}{x_C}$.即$E(2{y_C},-\frac{1}{2}{x_C})$,则$F(-2{y_C},\frac{1}{2}{x_C})$.
|CD|2+|EF|2=$4(x_C^2+y_C^2+y_E^2+x_E^2)$
=$4(x_C^2+y_C^2+4y_C^2+\frac{1}{4}x_C^2)$
=$4[{4+\frac{1}{4}(x_C^2+4y_C^2)}]$.
又$x_C^2+4y_C^2=4$,所以|CD|2+|EF|2=20.
点评 本题考查椭圆的方程和性质,存在性问题的解法和直线的斜率公式的运用,同时考查直线和椭圆方程联立,考查化简整理的运算能力,属于中档题.

| A. | 若m∥α,n∥α,则m∥n | B. | 若m∥α,m∥β,则α∥β | ||
| C. | 若m∥α,n∥β,m∥n,则α∥β | D. | 若α∥β,α∩γ=m,β∩γ=n,则m∥n |

| A. | 15 | B. | 23 | C. | 47 | D. | 95 |
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 1 | D. | 2 |
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
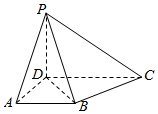 在四棱锥P-ABCD中,AD⊥平面PDC,PD⊥DC,底面ABCD是梯形,AB∥DC,AB=AD=PD=1,CD=2.
在四棱锥P-ABCD中,AD⊥平面PDC,PD⊥DC,底面ABCD是梯形,AB∥DC,AB=AD=PD=1,CD=2.