题目内容
19.一个正方体的平面展开图及该正方体的直观图如图所示,在正方体中,设AB终点为M,CF中点为N.
(1)请将字母F、G、H标记在正方体相应的顶点处(不需说明理由);
(2)证明:直线MN∥面AEF;
(3)若正方体棱长为2,求三棱锥M-AEF的体积.
分析 (1)将正方体的平面展开图还胡成该正方体的直观图,能将字母F、G、H标记在正方体相应的顶点处.
(2)设P为BE中点,推导出面MNP∥面AEF,由此能证明MN∥面AEF.
(3)三棱锥M-AEF的体积VM-AEF=VF-AEM,由此能求出结果.
解答 解:(1)将正方体的平面展开图还胡成该正方体的直观图,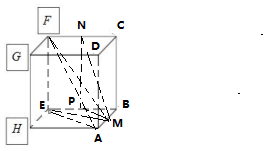
将字母F、G、H标记在正方体相应的顶点处,如右图:
证明:(2)设P为BE中点,连MP、NP,
∵N为CF中点,
∴NP∥EF,NP?面AEF,EF?面AEF,
∴NP∥面AEF,
又∵M为AB中点,∴MP$\underset{∥}{=}$$\frac{1}{2}$AE,
∵MP?面AEF,AE?面MNP,
∴MP∥面AEF,
而MP∩NP=P,MP、NP?面MNP,
∴面MNP∥面AEF,
∵MN?面MNP,
∴MN∥面AEF.
解:(3)∵正方体棱长为2,
∴三棱锥M-AEF的体积:
VM-AEF=VF-AEM=$\frac{1}{3}×{S}_{△AEM}×EF$=$\frac{1}{3}×\frac{1}{2}×1×2×2=\frac{2}{3}$.
点评 本题考查正方形结构特征的应用,考查线面平行的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
14.A为圆O:x2+y2=1上的点,B为直线l:x+y-2=0上的点,则线段AB长度的最小值为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{2}$-1 | D. | 1 |
 如图,已知E、F两点分别是正方形ABCD边AD、AB的中点,EF交AC于点M,GC垂直于ABCD所在平面.
如图,已知E、F两点分别是正方形ABCD边AD、AB的中点,EF交AC于点M,GC垂直于ABCD所在平面.