题目内容
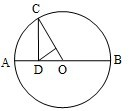（2013•湖北）（选修4-1：几何证明选讲）如图，圆O上一点C在直径AB上的射影为D，点D在半径OC上的射影为E．若AB=3AD，则
| CE | EO |
8
8
．分析：设圆O的半径为3x，根据射影定理，可以求出OD2=OE•OC=x2，CD2=CE•OC=8x2，进而得到
的值．
| CE |
| EO |
解答：解：设圆O的半径OA=OB=OC=3x，
∵AB=3AD，
∴AD=2x，BD=4x，OD=x
又∵点C在直径AB上的射影为D，
在△ABC中，由射影定理得：CD2=AD•BD=8x2，
在△ODC中，由射影定理得：OD2=OE•OC=x2，CD2=CE•OC=8x2，
故
=
=8
故答案为：8
∵AB=3AD，
∴AD=2x，BD=4x，OD=x
又∵点C在直径AB上的射影为D，
在△ABC中，由射影定理得：CD2=AD•BD=8x2，
在△ODC中，由射影定理得：OD2=OE•OC=x2，CD2=CE•OC=8x2，
故
| CE |
| EO |
| CD2 |
| OD2 |
故答案为：8
点评：本题考查的知识点是直角三角形射影定理，射影定理在使用时一定要注意其使用范围…“双垂直”．
练习册系列答案
阅读快车系列答案
相关题目