题目内容
下列函数①
；②f（x）=sin2x；③f（x）=2-|x|；④f（x）=tanx中，满足“存在与x无关的正常数M，使得|f（x）|≤M对定义域内的一切实数x都成立”的有
- A.①②
- B.③④
- C.②③
- D.①④
C
分析：的值域为（-∞，0）∪（0，+∞），①显然不满足；同样f（x）=tanx的值域为R，也不行；④由正弦函数的有界性，可判断②，由指数函数的性质可判断③，从而可得答案．
解答：∵的值域为（-∞，0）∪（0，+∞），故①不满足；
f（x）=sin2x≤1，不妨取M=2，则|f（x）|≤2对定义域内的一切实数x都成立，故②满足；
f（x）=2-|x|；=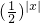
≤1，显然③满足题意；
而f（x）=tanx的值域为（-∞，+∞），故④不满足．
故选C．
点评：本题考查三角函数的最值，指数函数与幂函数的性质，关键是对条件的理解与各个函数性质的掌握与应用，属于中档题．
分析：
的值域为（-∞，0）∪（0，+∞），①显然不满足；同样f（x）=tanx的值域为R，也不行；④由正弦函数的有界性，可判断②，由指数函数的性质可判断③，从而可得答案．解答：∵
的值域为（-∞，0）∪（0，+∞），故①不满足；f（x）=sin2x≤1，不妨取M=2，则|f（x）|≤2对定义域内的一切实数x都成立，故②满足；
f（x）=2-|x|；=
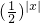≤1，显然③满足题意；而f（x）=tanx的值域为（-∞，+∞），故④不满足．
故选C．
点评：本题考查三角函数的最值，指数函数与幂函数的性质，关键是对条件的理解与各个函数性质的掌握与应用，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
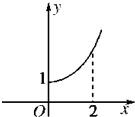定义在R上的偶函数f（x）的部分图象如图所示，则在（-2，0）上，下列函数中与f（x）的单调性不同的是（ ）| A、y=x2+1 | |||||
| B、y=|x|+1 | |||||
C、y=
| |||||
D、y=
|
已知甲、乙两个工厂在今年的1月份的利润都是6万元，且甲厂在2月份的利润是14万元，乙厂在2月份的利润是8万元．若甲、乙两个工厂的利润（万元）与月份之间的函数关系式分别符合下列函数模型：f（x）=a1x2+b1x+6，g（x）=a2•3x+b2，（a1，a2，b1，b2∈R）下列函数中，f（x）的最小值为4的是（ ）
A、f(x)=x+
| ||||
B、f(x)=
| ||||
C、f(x)=sin2x+
| ||||
| D、f（x）=2（3x+3-x） |