题目内容
下列函数中，f（x）的最小值为4的是（ ）
A、f(x)=x+
| ||||
B、f(x)=
| ||||
C、f(x)=sin2x+
| ||||
| D、f（x）=2（3x+3-x） |
分析：通过给变量取特殊值，举反例可得到有3个选项不正确，故可排除掉，剩下的一个选项可用基本不等式进行证明．
解答：解：当x＜0时，A显然不满足条件． 当
=1时，B取最小值，而方程
=1无解，显然不满足条件．
当sin2x=2时，C取最小值，而方程sin2x=2无解，C显然不满足条件．
∵3x＞0，∴2（3x+
）≥2×2
=4，
故只有D 满足条件，
故选D．
| x2+4 |
| x2+4 |
当sin2x=2时，C取最小值，而方程sin2x=2无解，C显然不满足条件．
∵3x＞0，∴2（3x+
| 1 |
| 3x |
3x•
|
故只有D 满足条件，
故选D．
点评：本题考查基本不等式的应用，通过给变量取特殊值，举反例来说明某个命题不正确，是一种简单有效的方法．
练习册系列答案
53随堂测系列答案
相关题目
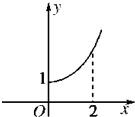定义在R上的偶函数f（x）的部分图象如图所示，则在（-2，0）上，下列函数中与f（x）的单调性不同的是（ ）| A、y=x2+1 | |||||
| B、y=|x|+1 | |||||
C、y=
| |||||
D、y=
|