题目内容
已知数列{an}的前n项和为Sn,数列{bn}中,b1=a1,bn=an-an-1(n≥2),且an+Sn=n.
(1)设cn=an-1,求证:{cn}是等比数列;
(2)求数列{bn}的通项公式.
解析 (1)证明 ∵an+Sn=n,①
∴an+1+Sn+1=n+1.②
②-①得an+1-an+an+1=1,
∴2an+1=an+1,∴2(an+1-1)=an-1,
∴ =
=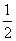 ,∴{an-1}是等比数列.
,∴{an-1}是等比数列.
∵首项c1=a1-1,又a1+a1=1.
∴a1=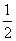 ,∴c1=-
,∴c1=-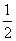 ,公比q=
,公比q=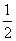 .
.
又cn=an-1,
∴{cn}是以-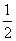 为首项,公比为
为首项,公比为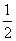 的等比数列.
的等比数列.
(2)由(1)可知cn=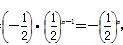 ,
,
∴an=cn+1=1-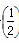 n.
n.
∴当n≥2时,bn=an-an-1=1-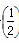 n
n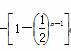
=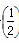 n-1-
n-1-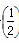 n=
n=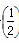 n.
n.
又b1=a1=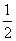 代入上式也符合,∴bn=
代入上式也符合,∴bn=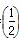 n.
n.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 且
且 = .
= .

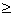 2,n
2,n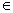 N+), 则bn=
N+), 则bn=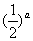 =
=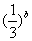 ,则a>b>0;
,则a>b>0;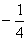 ;
; , 若目标函数z=ax+by(a>0,b>0)的值是最大值为12,则
, 若目标函数z=ax+by(a>0,b>0)的值是最大值为12,则 的最小值为( )
的最小值为( ) C.
C.  D. 7
D. 7 体积是 ( )
体积是 ( )