题目内容
如图，在正方体ABCD-A1B1C1D1中，E是AA1的中点，（Ⅰ）求直线BC与A1C所成的角的度数．
（Ⅱ）求证：A1C∥平面BDE．
考点：异面直线及其所成的角,直线与平面平行的判定
专题：空间位置关系与距离
分析：（I）利用正方体的性质和直角三角形的边角关系即可得出；
（II）利用三角形的中位线定理和线面平行的判定定理即可得出．
（II）利用三角形的中位线定理和线面平行的判定定理即可得出．
解答：
（I）解：如图所示，不妨设正方体的棱长AB=1．连接BA1．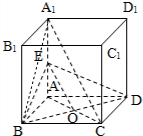
由正方体可得：BC⊥BA1．
∵A1B=
，∴tan∠A1BC=
=
．
∴∠BCA1=arctan
．
（Ⅱ）证明：在正方体ABCD-A1B1C1D1中，连接AC交BD于点O，连接EO，
则O为AC的中点，又E是的AA1的中点，
∴EO为△A1AC为的中位线，
∴EO∥A1C，
∵EO?平面BED，A1C?平面BED，
∴A1C∥平面BED．
由正方体可得：BC⊥BA1．
∵A1B=
| 2 |
| A1B |
| BC |
| 2 |
∴∠BCA1=arctan
| 2 |
（Ⅱ）证明：在正方体ABCD-A1B1C1D1中，连接AC交BD于点O，连接EO，
则O为AC的中点，又E是的AA1的中点，
∴EO为△A1AC为的中位线，
∴EO∥A1C，
∵EO?平面BED，A1C?平面BED，
∴A1C∥平面BED．
点评：（I）利用正方体的性质和直角三角形的边角关系即可得出；
（II）利用三角形的中位线定理和线面平行的判定定理即可得出．
（II）利用三角形的中位线定理和线面平行的判定定理即可得出．
练习册系列答案
教材全解字词句篇系列答案
相关题目
甲、乙、丙、丁、戊五人并排站成一排，如果甲必须站在乙的右边（甲、乙可以不相邻）那么不同的排法共有（ ）
| A、24种 | B、60种 |
| C、90种 | D、120种 |
某校高一年级60名学生参加数学竞赛，成绩全部在40分至100分之间，现将成绩分成以下6段：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]，据此绘制了如图所示的频率分布直方图．