题目内容
已知等差数列 的首项
的首项 公差
公差 且
且 分别是等比数列
分别是等比数列 的
的
(1)求数列 和
和 的通项公式;
的通项公式;
(2)设数列 对任意正整数
对任意正整数 均有
均有 成立,求
成立,求 的值.
的值.
(1) ,
, ; (2)
; (2)
解析试题分析:(1)根据等差数列的首项和公差求通项公式;(2)根据等比数列的首项和公比求通项公式;注意题中限制条件;(3)数列的递推关系是给出数列的一种方法,根据给出的初始值和递推关系可以依次写出这个数列的各项,再由递推关系求数列的通项公式,常用方法有:一是求出数列的前几项,再归纳总结出数列的一个通项公式;二是将已知递推关系式整理、变形,变成等差数列或者等比数列,或用累加法,累乘法,迭代法求通项.
试题解析:(1)∵ ,且
,且 成等比数列,
成等比数列,
∴ ,即
,即 ,∴
,∴ 4分
4分
又∵ ∴
∴ 6分
6分
(2)∵ , 1)
, 1)

 又
又 2)
2)
1)-2)得


则
=3+2
=
考点:等差数列与等比数列通项公式,由递推公式求通项公式及等比数列的前n项和公式

练习册系列答案
相关题目
根据下列算法语句,当输入x为60时,输出y的值为
| A.25 | B.30 | C.31 | D.61 |
已知直线 与直线
与直线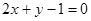 垂直,则
垂直,则 的值为( )
的值为( )
A. | B.0 | C. | D. |
 在区间
在区间 上的最大值是2,求实数
上的最大值是2,求实数 的值.
的值. 的夹角为
的夹角为 ,
, ,则
,则 的值是 _____
的值是 _____ ,动点
,动点 与
与 分别在射线
分别在射线 上,且线段
上,且线段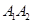 的长为1,线段
的长为1,线段 分别是线段
分别是线段 的中点.
的中点.
 与
与 表示向量
表示向量 ;
; 的最小值是 .
的最小值是 .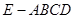 中,底面
中,底面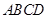 是正方形,
是正方形, 与
与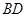 交于点
交于点 ,
,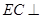 底面
底面 ,
, 为
为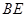 的中点.
的中点. 
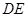 ∥平面
∥平面 ;
;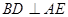 ;
; 在线段
在线段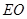 上是否存在点
上是否存在点 ,使
,使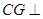 平面
平面 ?
?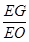 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.