题目内容
(本小题满分13分)函数 (
( 为常数)的图象过点
为常数)的图象过点 .
.
(1)求 的值;
的值;
(2)函数 在区间
在区间 上有意义,求实数
上有意义,求实数 的取值范围;
的取值范围;
(3)讨论关于 的方程
的方程 (
( 为常数)的正根的个数.
为常数)的正根的个数.
(1) ;(2)
;(2) ;(3)3个.
;(3)3个.
【解析】
试题分析:(1)依题意直接代入得 ;(2)将
;(2)将 代入得
代入得 ,要使其在区间
,要使其在区间 上有意义,只需满足
上有意义,只需满足 对
对 恒成立,得
恒成立,得 ,令
,令 ,先确定
,先确定 在
在 上的单调性(可利用求导,也可利用定义),再求
上的单调性(可利用求导,也可利用定义),再求 在
在 上的最小值,即可得到实数
上的最小值,即可得到实数 的取值范围;(3)求方程
的取值范围;(3)求方程 (
( 为常数)的正根的个数,可以转化为求函数
为常数)的正根的个数,可以转化为求函数 与
与 图像交点个数,其中
图像交点个数,其中 的图像和
的图像和 的大小有关,所以要分
的大小有关,所以要分 ,
, ,
, 三种情况讨论,详见解析.
三种情况讨论,详见解析.
试题解析:(1)依题意有 . 3分
. 3分
(2)由(1)得 ,则
,则 在区间
在区间 上有意义,即
上有意义,即 对
对 恒成立,得
恒成立,得 ,令
,令 ,
, 先证其单调递增:
先证其单调递增:
法1∵  在
在 上恒成立,故
上恒成立,故 在
在 递增,
递增,
法2: 任取 ,则
,则
因为 ,则
,则 ,故
,故 在
在 递增,则
递增,则 ,得
,得 . 8分
. 8分
(3)结合图象有:

①当 时,正根的个数为0;
时,正根的个数为0;
如图一
②当 时,正根的个数为1;
时,正根的个数为1;
如图二
③当 时,正根的个数为2;
时,正根的个数为2;
如图三 13分
考点:(1)待定系数法;(2)导数的应用及恒成立问题;(3)函数图像.

练习册系列答案
相关题目
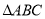 中,
中,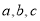 分别是角A,B,C的对边,若
分别是角A,B,C的对边,若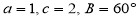 ,则
,则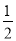 B.
B.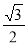 C.1 D.
C.1 D.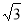
 与直线
与直线 平行,则它们之间的距离为( )
平行,则它们之间的距离为( ) B.
B. C.
C. D.
D.
 ,函数
,函数 在区间
在区间 上是( )
上是( ) B.增函数且
B.增函数且
 D.减函数且
D.减函数且
 的倾斜角是( )
的倾斜角是( )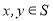 ,都有
,都有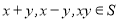 ,则称S为封闭集。下列命题:
,则称S为封闭集。下列命题: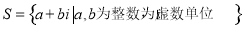 为封闭集;
为封闭集;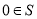 ;
;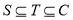 的任意集合
的任意集合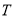 也是封闭集.
也是封闭集.  表示的曲线为( )
表示的曲线为( ) =
= 若函数
若函数 有3个零点,则实数
有3个零点,则实数 的取值范围是________.
的取值范围是________. 的二面角
的二面角  内一点,PA
内一点,PA  平面
平面  ,PB
,PB  ,A、B为垂足若PA=4.PB=2,则AB的长为_______.
,A、B为垂足若PA=4.PB=2,则AB的长为_______.