题目内容
已知已知函数 ,数列{an}满足a1=1,an+1=f(an)(n∈N*).
,数列{an}满足a1=1,an+1=f(an)(n∈N*).
(Ⅰ)求证:数列 是等差数列;
是等差数列;
(Ⅱ)记Sn=a1a2+a2a3+…+anan+1,试比较2Sn与1的大小.
解:(Ⅰ)由已知得,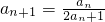 ,
,
∴ ,即
,即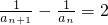 .
.
∴数列 是首项,公差d=2的等差数列.(6分)
是首项,公差d=2的等差数列.(6分)
(Ⅱ)由(Ⅰ)知 ,
,
∴ ,(8分)
,(8分)
∴ ,(10分)
,(10分)
∴Sn=a1a2+a2a3++anan+1=
= =
=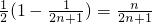 .(14分)
.(14分)
∴ (n∈N*),∴2Sn<1.(16分)
(n∈N*),∴2Sn<1.(16分)
分析:本题考查了函数和数列的关系、等差数列的证明、数列的求和等知识点.
(Ⅰ)根据所给函数 及数列{an}满足a1=1,an+1=f(an)(n∈N*)即可获得{an}的递推关系,然后通过推出
及数列{an}满足a1=1,an+1=f(an)(n∈N*)即可获得{an}的递推关系,然后通过推出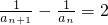 得到证明.
得到证明.
(Ⅱ)在(Ⅰ)的基础上易得anan+1= ,由此不难想到“裂项法”求和.
,由此不难想到“裂项法”求和.
点评:本题综合性较强,涉及了多个知识点的融合,揭示了函数和数列的内在联系,并且在构造数列,证明等差数列,裂项求和等方面设计了很好的情景,是一个培养逻辑推理能力和思维能力的好题,而且也代表了目前高考试题的方向.
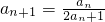 ,
,∴
 ,即
,即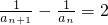 .
.∴数列
 是首项,公差d=2的等差数列.(6分)
是首项,公差d=2的等差数列.(6分)(Ⅱ)由(Ⅰ)知
 ,
,∴
 ,(8分)
,(8分)∴
 ,(10分)
,(10分)∴Sn=a1a2+a2a3++anan+1=

=
 =
=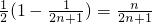 .(14分)
.(14分)∴
 (n∈N*),∴2Sn<1.(16分)
(n∈N*),∴2Sn<1.(16分)分析:本题考查了函数和数列的关系、等差数列的证明、数列的求和等知识点.
(Ⅰ)根据所给函数
 及数列{an}满足a1=1,an+1=f(an)(n∈N*)即可获得{an}的递推关系,然后通过推出
及数列{an}满足a1=1,an+1=f(an)(n∈N*)即可获得{an}的递推关系,然后通过推出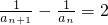 得到证明.
得到证明.(Ⅱ)在(Ⅰ)的基础上易得anan+1=
 ,由此不难想到“裂项法”求和.
,由此不难想到“裂项法”求和.点评:本题综合性较强,涉及了多个知识点的融合,揭示了函数和数列的内在联系,并且在构造数列,证明等差数列,裂项求和等方面设计了很好的情景,是一个培养逻辑推理能力和思维能力的好题,而且也代表了目前高考试题的方向.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
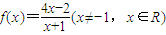 ,数列{an}满足 a1=a(a≠-1,a∈R),an+1=f(an)(n∈N*).
,数列{an}满足 a1=a(a≠-1,a∈R),an+1=f(an)(n∈N*). ,证明数列{bn}是等比数列,并求出通项公式an.
,证明数列{bn}是等比数列,并求出通项公式an. ,数列{an}满足a1=a(a≠-2,a∈R),an+1=f(an)(n∈N*).
,数列{an}满足a1=a(a≠-2,a∈R),an+1=f(an)(n∈N*). ,证明数列{bn}是等比数列,并求出通项公式an.
,证明数列{bn}是等比数列,并求出通项公式an.