题目内容
已知函数 ,数列{an}满足a1=a(a≠-2,a∈R),an+1=f(an)(n∈N*).
,数列{an}满足a1=a(a≠-2,a∈R),an+1=f(an)(n∈N*).(1)若数列{an}是常数列,求a的值;
(2)当a1=2时,记
 ,证明数列{bn}是等比数列,并求出通项公式an.
,证明数列{bn}是等比数列,并求出通项公式an.
【答案】分析:(1)由数列{an}是常数列,知a2=f(a1)=a,解方程即得a的值;
(2)由 ,知
,知 ,由an+1=f(an)再化简整理,得
,由an+1=f(an)再化简整理,得 ,即
,即 ,可证{bn}是等比数列,先求出{bn}的通项,再求通项公式an.
,可证{bn}是等比数列,先求出{bn}的通项,再求通项公式an.
解答:解(1)∵ ,且数列{an}是常数列,
,且数列{an}是常数列,
∴a2=a1=a,即 ,解得a=-1,或a=1.
,解得a=-1,或a=1.
∴所求实数a的值是1或-1.
(2)∵ ,
,
∴ ,即
,即 .
.
∴数列{bn}是以 为首项,公比为
为首项,公比为 的等比数列,于是
的等比数列,于是 .
.
由 ,即
,即 ,解得
,解得 .
.
∴所求的通项公式 .
.
点评:本题考查了常数列、等比数列以及数列通项公式的概念,也考查了方程的思想,转化构造的能力和计算能力.
(2)由
 ,知
,知 ,由an+1=f(an)再化简整理,得
,由an+1=f(an)再化简整理,得 ,即
,即 ,可证{bn}是等比数列,先求出{bn}的通项,再求通项公式an.
,可证{bn}是等比数列,先求出{bn}的通项,再求通项公式an.解答:解(1)∵
 ,且数列{an}是常数列,
,且数列{an}是常数列,∴a2=a1=a,即
 ,解得a=-1,或a=1.
,解得a=-1,或a=1.∴所求实数a的值是1或-1.
(2)∵
 ,
,∴
 ,即
,即 .
.∴数列{bn}是以
 为首项,公比为
为首项,公比为 的等比数列,于是
的等比数列,于是 .
.由
 ,即
,即 ,解得
,解得 .
.∴所求的通项公式
 .
.点评:本题考查了常数列、等比数列以及数列通项公式的概念,也考查了方程的思想,转化构造的能力和计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,数列an满足
,数列an满足 .
.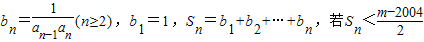 对一切n∈N*成立,求最小正整数m.
对一切n∈N*成立,求最小正整数m.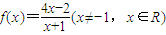 ,数列{an}满足 a1=a(a≠-1,a∈R),an+1=f(an)(n∈N*).
,数列{an}满足 a1=a(a≠-1,a∈R),an+1=f(an)(n∈N*). ,证明数列{bn}是等比数列,并求出通项公式an.
,证明数列{bn}是等比数列,并求出通项公式an. 若数列{an}满足an=
若数列{an}满足an= (n∈N+)且{an}是递减数列,则实数a的取值范围是( )
(n∈N+)且{an}是递减数列,则实数a的取值范围是( ) ,1) B.(
,1) B.(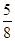 ) C.(
) C.( ) D.(
) D.( ,数列an满足an=f(n)(n∈N*),且an是递增数列,则实数a的取值范围是
,数列an满足an=f(n)(n∈N*),且an是递增数列,则实数a的取值范围是