题目内容
函数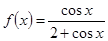 的值域是______.
的值域是______.
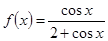 的值域是______.
的值域是______. .
.试题分析:
 表示的几何意义是点A(2,0),B(-cosx,-cosx)两点连线的斜率,因为点B在线段y=x,
表示的几何意义是点A(2,0),B(-cosx,-cosx)两点连线的斜率,因为点B在线段y=x, 上,所以
上,所以 ,即
,即 .
.点评:解本小题的关键是把
 看作点A(2,0),B(-cosx,-cosx)两点连线的斜率,然后再根据动点B的轨迹是线段y=x,
看作点A(2,0),B(-cosx,-cosx)两点连线的斜率,然后再根据动点B的轨迹是线段y=x, ,数形结合可求得f(x)的范围。
,数形结合可求得f(x)的范围。
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
题目内容
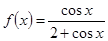 的值域是______.
的值域是______. .
. 表示的几何意义是点A(2,0),B(-cosx,-cosx)两点连线的斜率,因为点B在线段y=x,
表示的几何意义是点A(2,0),B(-cosx,-cosx)两点连线的斜率,因为点B在线段y=x, 上,所以
上,所以 ,即
,即 .
. 看作点A(2,0),B(-cosx,-cosx)两点连线的斜率,然后再根据动点B的轨迹是线段y=x,
看作点A(2,0),B(-cosx,-cosx)两点连线的斜率,然后再根据动点B的轨迹是线段y=x, ,数形结合可求得f(x)的范围。
,数形结合可求得f(x)的范围。
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案