Question

4．如图所示，长方体ABCD-A₁B₁C₁D₁中，M、N分别为AB、A₁D₁的中点，判断MN与平面A₁BC₁的位置关系，并证明你的理由．

Answer 1

分析 以D为原点，DA为x轴，DC为y轴，DD₁为z轴，建立空间直角坐标系，利用向量法能证明MN∥平面A₁BC₁．

解答 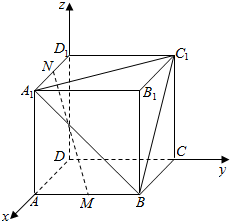解：MN∥平面A₁BC₁．
证明如下：
以D为原点，DA为x轴，DC为y轴，DD₁为z轴，建立空间直角坐标系，
设AD=a，AB=b，AA₁=c，
则M（a，$\frac{b}{2}$，0），N（$\frac{a}{2}$，0，c），A₁（a，0，c），B（a，b，0），C₁（0，b，c），
∴$\overrightarrow{MN}$=（-$\frac{a}{2}$，-$\frac{b}{2}$，c），$\overrightarrow{{A}_{1}B}$=（0，b，-c），$\overrightarrow{{A}_{1}{C}_{1}}$=（-a，b，0），
设平面A₁BC₁的法向量$\overrightarrow{n}$=（x，y，z），
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{{A}_{1}B}=by-cz=0}\\{\overrightarrow{n}•\overrightarrow{{A}_{1}{C}_{1}}=-ax+by=0}\end{array}\right.$，取x=1，得$\overrightarrow{n}$=（1，$\frac{a}{b}$，$\frac{a}{c}$），
∵$\overrightarrow{MN}•\overrightarrow{n}$=-$\frac{a}{2}$-$\frac{a}{2}$+a=0，MN?平面A₁BC₁，
∴MN∥平面A₁BC₁．

点评 本题考查直线与平面的位置关系的判断与证明，是中档题，解题时要认真审题，注意向量法的合理运用．