题目内容
19.(本小题12分)设圆上的点A(2,3)关于直线x+2y=0的对称点仍在圆上,且与直线x-y+1=0相交的弦长为![]() ,求圆的方程.
,求圆的方程.
(x-6)2+(y+3)2=52或(x-14)2+(y+7)2=244
解析:
设圆的方程为(x-a)2+(y-b)2=r2.
∵圆上的点A(2,3)关于直线x+2y=0的对称点仍在圆上,
∴圆心在x+2y=0上. ∴a+2b=0. ①
∵圆被直线截得的弦长为![]() , ∴(
, ∴(![]() )2+(
)2+(![]() )2=r2. ②
)2=r2. ②
由点A(2,3)在圆上,得(2-a)2+(3-b)2=r2. ③
联立①②③,解得
∴圆的方程为(x-6)2+(y+3)2=52或(x-14)2+(y+7)2=244.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 )(t∈R , t ≠ 0)为圆心的圆与
)(t∈R , t ≠ 0)为圆心的圆与 轴交于点O, A,
轴交于点O, A, ,求圆C的方程.
,求圆C的方程. ,
, 是抛物线
是抛物线 的焦点,过点
的焦点,过点 与
与 、
、 两点,
两点, 为坐标原点.
为坐标原点. 为直径的圆的方程;
为直径的圆的方程; ,求直线
,求直线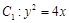 的焦点到准线的距离与椭圆
的焦点到准线的距离与椭圆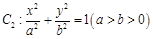 的长半轴相等,设椭圆的右顶点为
的长半轴相等,设椭圆的右顶点为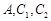 在第一象限的交点为
在第一象限的交点为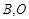 为坐标原点,且
为坐标原点,且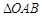 的面积为
的面积为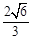
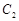 的标准方程;
的标准方程; 作直线
作直线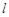 交
交 于
于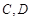 两点,射线
两点,射线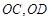 分别交
分别交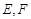 两点.
两点.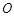 点在以
点在以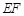 为直径的圆的内部;
为直径的圆的内部;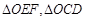 的面积分别为
的面积分别为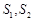 ,问是否存在直线
,问是否存在直线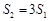 ?请说明理由.
?请说明理由.
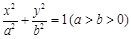 的长轴为
的长轴为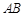 ,过点
,过点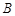 的直线
的直线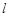 与
与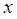 轴垂直.直线
轴垂直.直线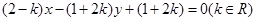 所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率
所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率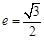 。
。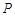 是椭圆上异于
是椭圆上异于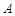 、
、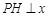 轴,
轴,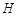 为垂足,延长
为垂足,延长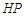 到点
到点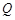 使得
使得 ,连结
,连结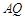 延长交直线
延长交直线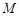 ,
, 为
为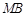 的中点.试判断直线
的中点.试判断直线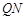 与以
与以 的位置关系。
的位置关系。
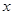 轴交于点O, A, 与y轴交于点O, B, 其中O为原点.
轴交于点O, A, 与y轴交于点O, B, 其中O为原点.