题目内容
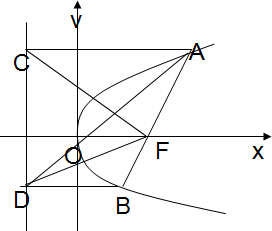
 抛物线y2=2px(p>0)的焦点为F,准线为l,过F的直线交抛物线于A(x1,y1)、B(x2,y2)两点,AC垂直准线于C,BD垂直准线于D,又O为原点.
抛物线y2=2px(p>0)的焦点为F,准线为l,过F的直线交抛物线于A(x1,y1)、B(x2,y2)两点,AC垂直准线于C,BD垂直准线于D,又O为原点.(1)证明:CF⊥DF
(2)A、O、D三点共线
(3)
| 1 |
| AF |
| 1 |
| BF |
| 2 |
| p |
考点:直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:(1)首先根据抛物线的定义,证明三角形ACF是等腰三角形;然后证明CF平分∠OFA,同理DF平分∠OFB,据此判断出CF⊥DF即可;
(2)首先求出抛物线的焦点坐标,然后得到经过点F的直线的方程,代入到抛物线方程中,消去x得到关于y的一元二次方程,进而得到两根之积;然后根据BD∥x轴与点D在准线上可求得D的坐标,进而表示出直线DO的斜率,同时可得到k也是直线OA的斜率,据此证明即可;
(3)首先设过F的直线方程,与抛物线方程联立,整理后,根据韦达定理可求得x1x2的值;然后根据抛物线定义可知,|AF|=x1+
,|BF|=x2+
,代入证明结论即可.
(2)首先求出抛物线的焦点坐标,然后得到经过点F的直线的方程,代入到抛物线方程中,消去x得到关于y的一元二次方程,进而得到两根之积;然后根据BD∥x轴与点D在准线上可求得D的坐标,进而表示出直线DO的斜率,同时可得到k也是直线OA的斜率,据此证明即可;
(3)首先设过F的直线方程,与抛物线方程联立,整理后,根据韦达定理可求得x1x2的值;然后根据抛物线定义可知,|AF|=x1+
| p |
| 2 |
| p |
| 2 |
解答:
解:(1)如图,由抛物线的定义可知
AC=AF,三角形ACF是等腰三角形;
因为AC∥OF,
所以CF平分∠OFA,
同理DF平分∠OFB,
所以∠CFD=90°,
即CF⊥DF;
(2)因为抛物线y2=2px(p>0)的焦点为F(
,0),
所以设经过点F的直线的方程为x=my+
,
把它代入抛物线方程,可得y2-2pmy-p2=0;
因为A(x1,y1),B(x2,y2),
所以y1,y2是该方程的两个根,
则y1y2=-p2;
因为BD∥x轴,且点D在准线x=-
上,
所以点D的坐标为(-
,y2),
故直线DO的斜率为
=
=
,
即k也是直线OA的斜率,
所以直线AD经过原点O,
即A、O、D三点共线;
(3)设经过点F的直线的方程为y=k(x-
),
把它代入抛物线方程,可得4k2x2-4p(k2+2)x+p2=0;
因为A(x1,y1),B(x2,y2),
所以x1,x2是该方程的两个根,
则x1+x2=
,x1x2=
,
根据抛物线性质可知,
|AF|=x1+
,|BF|=x2+
,
所以
+
=
=
=2
因此
+
=
成立.
AC=AF,三角形ACF是等腰三角形;
因为AC∥OF,
所以CF平分∠OFA,
同理DF平分∠OFB,
所以∠CFD=90°,
即CF⊥DF;
(2)因为抛物线y2=2px(p>0)的焦点为F(
| p |
| 2 |
所以设经过点F的直线的方程为x=my+
| p |
| 2 |
把它代入抛物线方程,可得y2-2pmy-p2=0;
因为A(x1,y1),B(x2,y2),
所以y1,y2是该方程的两个根,
则y1y2=-p2;
因为BD∥x轴,且点D在准线x=-
| p |
| 2 |
所以点D的坐标为(-
| p |
| 2 |
故直线DO的斜率为
| y2 | ||
-
|
| 2p |
| y1 |
| y1 |
| x1 |
即k也是直线OA的斜率,
所以直线AD经过原点O,
即A、O、D三点共线;
(3)设经过点F的直线的方程为y=k(x-
| p |
| 2 |
把它代入抛物线方程,可得4k2x2-4p(k2+2)x+p2=0;
因为A(x1,y1),B(x2,y2),
所以x1,x2是该方程的两个根,
则x1+x2=
| p(k2+2) |
| k2 |
| p2 |
| 4k2 |
根据抛物线性质可知,
|AF|=x1+
| p |
| 2 |
| p |
| 2 |
所以
| 1 |
| AF |
| 1 |
| BF |
| x1+x2+p | ||||
(x1+
|
| ||||||||
|
因此
| 1 |
| AF |
| 1 |
| BF |
| 2 |
| p |

点评:本题主要考查了抛物线的概念和性质的运用,考查了直线的方程和性质,属于中档题.

练习册系列答案
相关题目
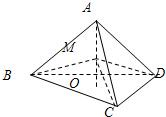 如图,已知AO是四面体ABCD的高,M是AO的中点,连接BM、CM、DM.求证:BM、CM、DM两两垂直.
如图,已知AO是四面体ABCD的高,M是AO的中点,连接BM、CM、DM.求证:BM、CM、DM两两垂直.