题目内容
设奇函数f（x）=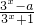
的反函数为f-1（x），则
- A.f--1（
）＞f--1（
） - B.f-1（3）＞f-1（2）
- C.f--1（）＜f-1（）
- D.f-1（3）＜f-1（2）
A
分析：要充分利用函数的奇偶性的概念，对于奇函数有一个结论：奇函数在x=0处有定义，则有f（0）=0，本题可以充分利用这一点来求参数a的值，然后求出反函数的定义域，用定义法判断其单调性，先在定义域上任取两个变量，且界定大小，再作差变形与零比较，得到f-1（x1）与f-1（x2）关系，可得结论．
解答：f（x）为奇函数，f（0）=
=0∴a=1
经检验，a=1时f（x）是奇函数
∴f（x）=y=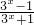
则3x=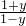
＞0∴-1＜y＜1
∴f-1（x）=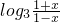
（x∈（-1，1）．
当-＜x1＜x2＜1时，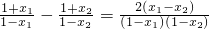
∵1-x1＞0，1-x2＞0，x1-x2＜0，
∴
，
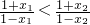于是：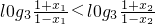
，
即：f-1（x1）＜f-1（x2）．
∴f-1（x）在（-1，1）上是增函数．
故选A．
点评：本题主要考查函数的反函数的求法及其单调性的判断，在求反函数时，要抓住x与y互换和原函数与反函数定义域与值域互换这两点．
分析：要充分利用函数的奇偶性的概念，对于奇函数有一个结论：奇函数在x=0处有定义，则有f（0）=0，本题可以充分利用这一点来求参数a的值，然后求出反函数的定义域，用定义法判断其单调性，先在定义域上任取两个变量，且界定大小，再作差变形与零比较，得到f-1（x1）与f-1（x2）关系，可得结论．
解答：f（x）为奇函数，f（0）=
=0∴a=1经检验，a=1时f（x）是奇函数
∴f（x）=y=
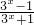
则3x=
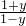＞0∴-1＜y＜1∴f-1（x）=
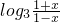（x∈（-1，1）．当-＜x1＜x2＜1时，
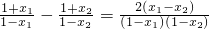
∵1-x1＞0，1-x2＞0，x1-x2＜0，
∴
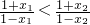，于是：
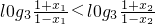，即：f-1（x1）＜f-1（x2）．
∴f-1（x）在（-1，1）上是增函数．
故选A．
点评：本题主要考查函数的反函数的求法及其单调性的判断，在求反函数时，要抓住x与y互换和原函数与反函数定义域与值域互换这两点．
练习册系列答案
相关题目
设奇函数f（x）在[-1，1]上是增函数，且f（-1）=-1，若函数f（x）≤t2-2at+1对所有的x∈[-1，1]都成立，则当a∈[-1，1]时，t的取值范围是（ ）
| A、-2≤t≤2 | ||||
B、-
| ||||
| C、t≥2或t≤-2或t=0 | ||||
D、t≥
|
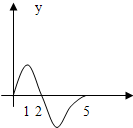（2013•铁岭模拟）设奇函数f（x）的定义域为[-5，5]，若x∈[0，5]时其图象如图，则不等式f（x）＜0的解集为