Question

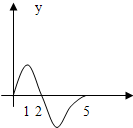（2013•铁岭模拟）设奇函数f（x）的定义域为[-5，5]，若x∈[0，5]时其图象如图，则不等式f（x）＜0的解集为

{x|-2＜x＜0，或2＜x＜5}

．

Answer 1

分析：先由图象求出当x＞0时不等式的解集，再由奇函数的性质求出当x＜0时不等式的解集，由此可得不等式的解集．

解答：解：由图象可知：当x＞0时，f（x）＜0⇒2＜x＜5，f（x）＞0⇒0＜x＜2；
当x＜0时，-x＞0，因为f（x）为奇函数，所以f（x）＜0⇒-f（-x）＜0⇒f（-x）＞0⇒0＜-x＜2，解得-2＜x＜0．
综上，不等式f（x）＜0的解集为{x|-2＜x＜0，或2＜x＜5}．
故答案为：{x|-2＜x＜0，或2＜x＜5}．

点评：本题考查奇函数的图象特征，属基础题，难度不大，本题也可利用奇函数图象关于原点对称作出y轴左侧的图象，根据图象写出解集．