题目内容
已知椭圆 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,直线y=
,直线y= x+1与椭圆相交于A、B两点,点M在椭圆上,
x+1与椭圆相交于A、B两点,点M在椭圆上, =
=
 +
+
 ,求椭圆的方程.
,求椭圆的方程.
 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,直线y=
,直线y= x+1与椭圆相交于A、B两点,点M在椭圆上,
x+1与椭圆相交于A、B两点,点M在椭圆上, =
=
 +
+
 ,求椭圆的方程.
,求椭圆的方程. +y2=1
+y2=1由e= 得a2=4b2,椭圆可化为:
得a2=4b2,椭圆可化为:
x2+4y2=4b2.
将y= x+1代入上式,消去y并整理得:
x+1代入上式,消去y并整理得:
x2+2x+2-2b2="0. " ①
∵直线y= x+1与椭圆交于A、B两点,
x+1与椭圆交于A、B两点,
∴Δ=4-4(2-2b2)>0,∴b> .
.
设A(x1,y1),B(x2,y2),M(x,y),则由
 =
=
 +
+
 ,
,
得 .
.
∵M在椭圆上,∴ (x1+
(x1+ x2)2+(y1+
x2)2+(y1+ y2)2=4b2,
y2)2=4b2,
∴x1x2+4y1y2=0.
∴x1x2+
 ·4=0,
·4=0,
即x1x2+(x1+x2)+2="0 " ②
又由①知x1+x2=-2,x1·x2=2-2b2,
代入②中得b2=1,满足b> .
.
∴椭圆方程为 +y2=1.
+y2=1.
 得a2=4b2,椭圆可化为:
得a2=4b2,椭圆可化为:x2+4y2=4b2.
将y=
 x+1代入上式,消去y并整理得:
x+1代入上式,消去y并整理得:x2+2x+2-2b2="0. " ①
∵直线y=
 x+1与椭圆交于A、B两点,
x+1与椭圆交于A、B两点,∴Δ=4-4(2-2b2)>0,∴b>
 .
.设A(x1,y1),B(x2,y2),M(x,y),则由
 =
=
 +
+
 ,
,得
 .
.∵M在椭圆上,∴
 (x1+
(x1+ x2)2+(y1+
x2)2+(y1+ y2)2=4b2,
y2)2=4b2,∴x1x2+4y1y2=0.
∴x1x2+

 ·4=0,
·4=0,即x1x2+(x1+x2)+2="0 " ②
又由①知x1+x2=-2,x1·x2=2-2b2,
代入②中得b2=1,满足b>
 .
.∴椭圆方程为
 +y2=1.
+y2=1.
练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
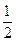 ,求顶点C的轨迹.
,求顶点C的轨迹.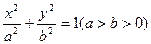
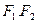
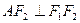
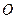
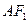
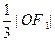
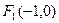 设过点
设过点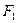 且不与坐标轴垂直的直线交椭圆于
且不与坐标轴垂直的直线交椭圆于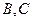 两点,线段
两点,线段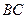 的垂直平分线与x轴交于
的垂直平分线与x轴交于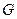 ,求点
,求点 与椭圆
与椭圆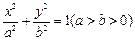 相交于
相交于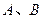 两点,且
两点,且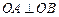 (其中
(其中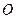 为坐标原点).(1)若椭圆的离心率为
为坐标原点).(1)若椭圆的离心率为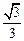 ,求椭圆的标准方程;
,求椭圆的标准方程;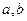 如何变化,椭圆恒过定点
如何变化,椭圆恒过定点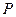
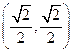 ;
;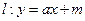 过(2)中的定点
过(2)中的定点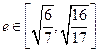 ,求原点到直线
,求原点到直线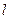 距离的取值范围.
距离的取值范围.
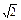 )且斜率为k的直线l与椭圆
)且斜率为k的直线l与椭圆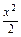 +y2=1有两个不同的交点P和Q.
+y2=1有两个不同的交点P和Q.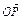 +
+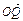 与
与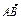 共线?如果存在,求k值;如果不存在,请说明理由.
共线?如果存在,求k值;如果不存在,请说明理由. 绕其左焦点逆时针方向旋转90°后所得椭圆方程是
绕其左焦点逆时针方向旋转90°后所得椭圆方程是 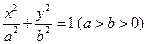 的面积为
的面积为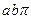 ,若全集
,若全集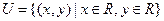 ,
,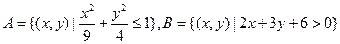 ,则
,则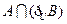 所表示的图形的面积为( ).
所表示的图形的面积为( ).

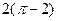
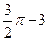
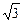 ,求椭圆方程.
,求椭圆方程.
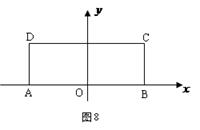
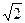 ,BC=1.以AB的中点
,BC=1.以AB的中点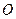 为原点建立如图8所示的平面直角坐标系
为原点建立如图8所示的平面直角坐标系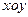 .
. 交(Ⅰ)中椭圆于M,N两点,是否存在直线
交(Ⅰ)中椭圆于M,N两点,是否存在直线