题目内容
已知一个圆的圆心为坐标原点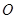 ,半径为
,半径为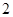 .从这个圆上任意一点
.从这个圆上任意一点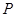 向
向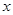 轴作垂线
轴作垂线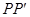 ,
,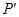 为垂足.
为垂足.
(Ⅰ)求线段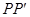 中点
中点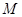 的轨迹方程;
的轨迹方程;
(Ⅱ)已知直线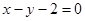 与
与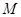 的轨迹相交于
的轨迹相交于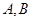 两点,求
两点,求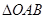 的面积
的面积
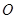 ,半径为
,半径为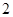 .从这个圆上任意一点
.从这个圆上任意一点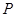 向
向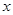 轴作垂线
轴作垂线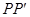 ,
,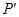 为垂足.
为垂足.(Ⅰ)求线段
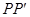 中点
中点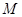 的轨迹方程;
的轨迹方程; (Ⅱ)已知直线
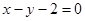 与
与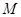 的轨迹相交于
的轨迹相交于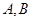 两点,求
两点,求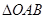 的面积
的面积(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)本题一般用动点转移法求轨迹方程,设动点
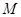 的坐标为
的坐标为 ,则点
,则点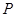 的坐标为
的坐标为 ,而点
,而点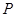 又是已知圆的点,把
又是已知圆的点,把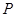 点坐标代入圆的方程即能求出动点
点坐标代入圆的方程即能求出动点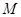 的轨迹方程;(2)直接列方程组求出交点
的轨迹方程;(2)直接列方程组求出交点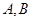 的坐标,然后选用相应面积公式计算面积(本题中以OB为底,高就是点A的纵坐标的绝对值).
的坐标,然后选用相应面积公式计算面积(本题中以OB为底,高就是点A的纵坐标的绝对值).试题解析:(1)设
 ,
, 则
则 1分
1分由中点公式得:
 3分
3分因为
 在圆上,
在圆上,
∴
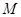 的轨迹方程为
的轨迹方程为 6分
6分(2)据已知
 8分
8分 10分
10分 12分
12分
练习册系列答案
相关题目
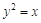 的焦点,S是抛物线C在第一象限内的点,且|SF|=
的焦点,S是抛物线C在第一象限内的点,且|SF|=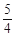 .
.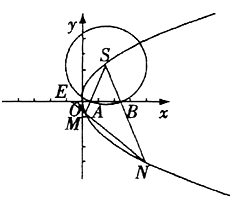
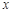 轴分别交于两点A、B,延长SA、SB分别交抛物线C于M、N两点;
轴分别交于两点A、B,延长SA、SB分别交抛物线C于M、N两点;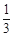 |NE|,求cos∠MSN的值.
|NE|,求cos∠MSN的值.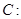
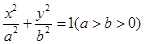 的离心率为
的离心率为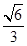 ,椭圆短轴的一个端点与两个焦点构成的三角形的面积为
,椭圆短轴的一个端点与两个焦点构成的三角形的面积为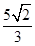 .
.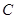 的方程;
的方程;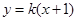 与椭圆
与椭圆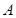 、
、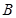 两点. ①若线段
两点. ①若线段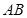 中点的横坐标为
中点的横坐标为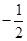 ,求斜率
,求斜率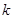 的值;②若点
的值;②若点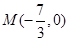 ,求证:
,求证: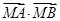 为定值.
为定值.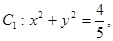 直线
直线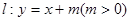 与圆
与圆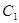 相切,且交椭圆
相切,且交椭圆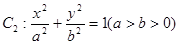 于
于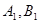 两点,
两点,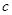 是椭圆的半焦距,
是椭圆的半焦距,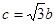 ,
,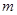 的值;
的值;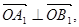 求椭圆
求椭圆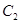 的方程;
的方程;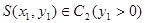 ,直线AS,BS与直线
,直线AS,BS与直线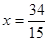 分别交于M,N两点,求线段MN的长度的最小值.
分别交于M,N两点,求线段MN的长度的最小值.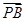 |,
|,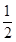 |
|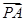 |,8成等差数列.
|,8成等差数列.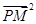 ,则称点M为点P对应的“比例点”.问:对任意一个确定的点P,它总能对应几个“比例点”?
,则称点M为点P对应的“比例点”.问:对任意一个确定的点P,它总能对应几个“比例点”?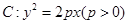 的焦点为
的焦点为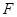 ,准线为
,准线为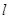 ,
,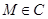 ,以
,以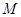 为圆心的圆
为圆心的圆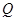 ,
,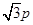 ,
,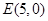 是圆
是圆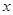 轴除
轴除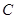 与圆
与圆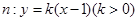 ,
,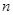 与
与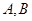 两点,
两点,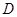 ,且
,且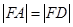 , 求
, 求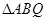 的面积.
的面积.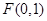 且与直线
且与直线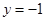 相切的动圆的圆心轨迹为
相切的动圆的圆心轨迹为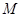 .点
.点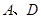 在轨迹
在轨迹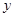 轴对称,过线段
轴对称,过线段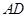 (两端点除外)上的任意一点作直线
(两端点除外)上的任意一点作直线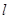 ,使直线
,使直线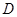 处的切线平行,设直线
处的切线平行,设直线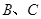 .
.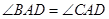 ;
;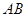 的距离等于
的距离等于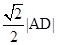 ,且
,且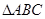 的面积为20,求直线
的面积为20,求直线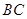 的方程.
的方程.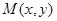 与定点
与定点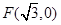 的距离和它到直线
的距离和它到直线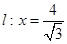 的距离之比是常数
的距离之比是常数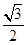 ,记
,记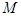 的轨迹为曲线
的轨迹为曲线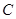 .
.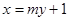 与曲线
与曲线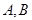 两点,点
两点,点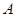 关于
关于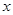 轴的对称点为
轴的对称点为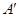 ,试问:当
,试问:当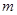 变化时,直线
变化时,直线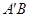 与
与 、
、 分别为双曲线
分别为双曲线 的左、右焦点,
的左、右焦点, 为双曲线的左顶点,以
为双曲线的左顶点,以 为直径的圆交双曲线某条渐过线
为直径的圆交双曲线某条渐过线 、
、 两点,且满足
两点,且满足 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )


