题目内容
12．
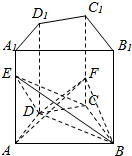如图，在直四棱柱ABCD-A1B1C1D1中，点E，F分别在AA1，CC1上，且AE=$\frac{4}{5}$AA1，CF=$\frac{1}{3}$CC1，点A，C到BD的距离之比为2：3，则三棱锥E-BCD和F-ABD的体积比$\frac{{V}_{E-BCD}}{{V}_{F-ABD}}$=$\frac{18}{5}$．
分析 利用距离比求出三角形的面积比，然后求解几何体的体积比．
解答 解：因为点A，C到BD的距离之比为2：3，所以$\frac{{S}_{△ABD}}{{S}_{△CBD}}=\frac{2}{3}$，
设AA1=a，则三棱锥E-BCD的高为$\frac{4a}{5}$，三棱锥F-ABD的高为$\frac{1}{3}a$，
故$\frac{{V}_{E-BCD}}{{V}_{F-ABD}}$=$\frac{3×\frac{4a}{5}}{2×\frac{1}{3}a}$=$\frac{18}{5}$．
故答案为：$\frac{18}{5}$．
点评 本题考查空间几何体的体积比的计算，考查空间想象能力以及计算能力．
练习册系列答案
阅读快车系列答案
相关题目
2．已知PA垂直于△ABC所在的平面，AB=AC=5，BC=6，PA=3，则点A到平面PBC的距离为（ ）
| A． | 4 | B． | $\sqrt{15}$ | C． | $3\sqrt{5}$ | D． | $\frac{12}{5}$ |
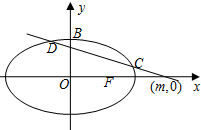如图，已知圆G：x2+y2-2x-$\sqrt{2}$y=0经过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点F及上顶点B，过椭圆外一点（m，0）（m＞a）且倾斜角为$\frac{5}{6}$π的直线l交椭圆于C，D两点．
在正棱柱ABCD一A1B1C1D1中，AA1=2AB，若E，F分别为线段A1D1，CC1的中点．求：