题目内容

3．已知三棱锥V-ABC，VA⊥平面ABC，在三角形ABC中，∠BAC=120°，AB=AC=VA=2，三棱锥V-ABC的外接球的表面积为（　　）
A．16πB．$\frac{32π}{3}$C．$\frac{20\sqrt{5}π}{3}$D．20π

分析 求出BC，可得△ABC外接圆的半径，从而可求该三棱锥的外接球的半径，即可求出三棱锥的外接球表面积．

解答 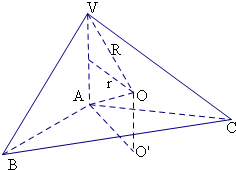解：∵AB=AC=2，∠BAC=120°，
∴BC=$\sqrt{{2}^{2}+{2}^{2}-2×2×2×（-\frac{1}{2}）}$=2$\sqrt{3}$，
∴三角形ABC的外接圆直径2r=$\frac{2\sqrt{3}}{sin120°}$=$\frac{2\sqrt{3}}{\frac{\sqrt{3}}{2}}$=4，
∴r=2，
∵VA⊥面ABC，VA=2，
由于三角形OVA为等腰三角形，
则有该三棱锥的外接球的半径R=$\sqrt{{r}^{2}+（\frac{1}{2}×2）^{2}}$=$\sqrt{5}$，
∴该三棱锥的外接球的表面积为S=4πR2=4π×（$\sqrt{5}$）2=20π．
故选：D．

点评 本题考查三棱锥的外接球表面积，考查直线和平面的位置关系，确定三棱锥的外接球的半径是关键．

练习册系列答案
相关题目
16．已知点A，B是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的顶点，P为双曲线上除顶点外的一点，记kPA，kPB分别表示直线PA，PB的斜率，若kPA•kPB=$\frac{5}{4}$，则该双曲线的离心率为（　　）
A．3B．2C．$\frac{3}{2}$D．$\frac{\sqrt{3}}{2}$
15．定义行列式运算 $|\begin{array}{l}{{a}_{1}}&{{a}_{2}}\\{{a}_{3}}&{a4}\end{array}|$=a1a4-a2a3．将函数f（x）=$|\begin{array}{l}{\sqrt{3}}&{sinx}\\{1}&{cosx}\end{array}|$的图象向左平移n（n＞0）个单位，所得图象对应的函数为偶函数，则n的最小值为 （　　）
A．$\frac{π}{6}$B．$\frac{5π}{6}$C．$\frac{π}{3}$D．$\frac{2π}{3}$
12．在直角坐标系xOy中，曲线M的参数方程为$\left\{\begin{array}{l}{x=\sqrt{3}cosα+sinα}\\{y=2\sqrt{3}sinαcosα-2si{n}^{2}α+2}\end{array}\right.$（α为参数），若以直角坐标系中的原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线N的极坐标方程为ρsin（θ+$\frac{π}{4}$）=$\frac{\sqrt{2}}{2}$t（t为参数）．
（Ⅰ）求曲线M和N的直角坐标方程；
（Ⅱ）若曲线N与曲线M有公共点，求t的取值范围．
19．若复数z满足（3-4i）z=5+10i，其中i为虚数单位，则z的虚部为（　　）
A．-2B．2C．-2iD．2i
8．要从由n名成员组成的小组中任意选派3人去参加某次社会调查．若在男生甲被选中的情况下，女生乙也被选中的概率为0.4，则n的值为（　　）
A．4B．5C．6D．7
15．在△ABC中，角A、B、C的对边分别为a、b、c，且$\frac{2sinC-sinB}{sinB}=\frac{{{a^2}+{c^2}-{b^2}}}{{{b^2}+{c^2}-{a^2}}}$．
（Ⅰ）求角A的大小；
（Ⅱ）若a=3，sinC=2sinB，求b、c的值．
12．已知焦点在x轴的椭圆方程：$\frac{x^2}{a^2}+{y^2}=1$，过焦点作垂直于x轴的直线交椭圆于A、B两点，且|AB|=1，则该椭圆的离心率为（　　）
A．$\frac{{\sqrt{3}}}{2}$B．$\frac{1}{2}$C．$\frac{{\sqrt{15}}}{4}$D．$\frac{{\sqrt{3}}}{3}$
11．已知直线l的斜率为2，M、N是直线l与双曲线C：$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1（a＞0，b＞0）$的两个交点，设M、N的中点为P（2，1），则C的离心率为（　　）
A．$\sqrt{2}$B．$\sqrt{3}$C．2D．2$\sqrt{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网