题目内容
12.已知焦点在x轴的椭圆方程:$\frac{x^2}{a^2}+{y^2}=1$,过焦点作垂直于x轴的直线交椭圆于A、B两点,且|AB|=1,则该椭圆的离心率为( )| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{15}}}{4}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
分析 求出椭圆的焦点坐标,利用|AB|=1,求出a、b、c,然后求解离心率即可.
解答 解:焦点在x轴的椭圆方程:$\frac{x^2}{a^2}+{y^2}=1$,焦点坐标(±$\sqrt{{a}^{2}-1}$,0),不妨A($\sqrt{{a}^{2}-1}$,$\frac{1}{2}$),
可得$\frac{{a}^{2}-1}{{a}^{2}}+\frac{1}{4}=1$,解得a=2,
椭圆的离心率为:e=$\frac{\sqrt{{a}^{2}-1}}{a}$=$\frac{\sqrt{3}}{2}$.
故选:A.
点评 本题考查椭圆的简单性质,离心率的求法,考查计算能力.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
3.设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点到一条渐近线的距离为a,则双曲线的离心率等于( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
3.已知三棱锥V-ABC,VA⊥平面ABC,在三角形ABC中,∠BAC=120°,AB=AC=VA=2,三棱锥V-ABC的外接球的表面积为( )
| A. | 16π | B. | $\frac{32π}{3}$ | C. | $\frac{20\sqrt{5}π}{3}$ | D. | 20π |
20.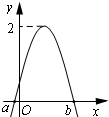 如图是函数$f(x)=Asin(2x+φ)(A>0,|φ|≤\frac{π}{2})$图象的一部分,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有$f({x_1}+{x_2})=\sqrt{3}$,则φ的值为( )
如图是函数$f(x)=Asin(2x+φ)(A>0,|φ|≤\frac{π}{2})$图象的一部分,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有$f({x_1}+{x_2})=\sqrt{3}$,则φ的值为( )
 如图是函数$f(x)=Asin(2x+φ)(A>0,|φ|≤\frac{π}{2})$图象的一部分,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有$f({x_1}+{x_2})=\sqrt{3}$,则φ的值为( )
如图是函数$f(x)=Asin(2x+φ)(A>0,|φ|≤\frac{π}{2})$图象的一部分,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有$f({x_1}+{x_2})=\sqrt{3}$,则φ的值为( )| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
7.把函数$y=5sin(2x-\frac{π}{6})$图象上所有点的横坐标伸长为原来的2倍(纵坐标不变),再把所得函数的图象向右平移$\frac{π}{3}$个单位,得到图象的解析式为( )
| A. | y=5cosx | B. | y=5cos4x | C. | y=-5cosx | D. | y=-5 cos4x |
19.设向量$\overrightarrow{a}$=(x,1),$\overrightarrow{b}$=(x,-4),则“$\overrightarrow{a}$⊥$\overrightarrow{b}$”是“x=2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
19.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线方程为y=±$\frac{1}{2}$x,则其离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
 已知抛物线y2=2px的焦点为F,若该抛物线上有一点A,满足直线FA的倾斜角为120°,且|FA|=4,
已知抛物线y2=2px的焦点为F,若该抛物线上有一点A,满足直线FA的倾斜角为120°,且|FA|=4,