题目内容
7.已知函数f(x)=|x2-2x|-a.(1)若函数f(x)没有零点,求实数a的取值范围;
(2)若函数f(x)有两个零点,求实数a的取值范围;
(3)若函数f(x)有三个零点,求实数a的取值范围;
(4)若函数f(x)有四个零点,求实数a的取值范围.
分析 作函数y=|x2-2x|的图象,函数f(x)=|x2-2x|-a的零点的个数可化为函数y=|x2-2x|的图象与直线y=a的图象的交点的个数,从而解得.
解答 解:作函数y=|x2-2x|的图象如下,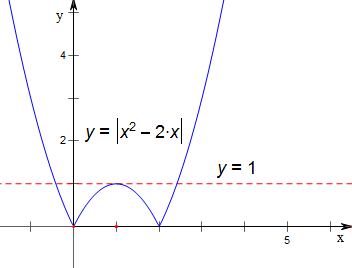
函数f(x)=|x2-2x|-a的零点的个数可化为函数y=|x2-2x|的图象与直线y=a的图象的交点的个数;
(1)当a<0时,函数f(x)没有零点;
(2)当a=0或a>1时,函数f(x)有两个零点;
(3)当a=1时,函数f(x)有三个零点;
(4)当0<a<1时,函数f(x)有四个零点.
点评 本题考查了学生的作图与应用图象的能力,同时考查了函数的零点与函数的图象的关系应用.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
17.若a>0,b>0,ab+a-b=2$\sqrt{2}$,则ab-a-b的值为( )
| A. | $\sqrt{6}$ | B. | 2或-2 | C. | -2 | D. | 2 |
2.下列四个函数中,既是偶函数又在(0,+∞)上为增函数的是( )
| A. | y=x2-2x | B. | y=x3 | C. | y=ln$\sqrt{1-{x}^{2}}$ | D. | y=|x|+1 |
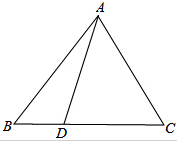 如图,△ABC中,|AB|=|AC|,D是BC边上任意一点,(D与B、C不重合),求证:|AB|2=|AD|2+|BD|•|DC|.
如图,△ABC中,|AB|=|AC|,D是BC边上任意一点,(D与B、C不重合),求证:|AB|2=|AD|2+|BD|•|DC|.