题目内容
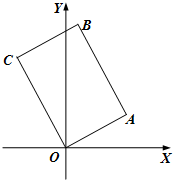 如图,已知四边形OABC是矩形,O是坐标原点,O、A、B、C按逆时针排列,A的坐标是(
如图,已知四边形OABC是矩形,O是坐标原点,O、A、B、C按逆时针排列,A的坐标是(| 3 |
(Ⅰ) 求点C的坐标;
(Ⅱ)求BC所在直线的方程.
分析:(Ⅰ) 求出OC所在想的斜率,推出OC的直线方程,利用|OC|的距离,求点C的坐标;
(Ⅱ)求出BC所在直线的斜率,利用点斜式求BC所在直线的方程.
(Ⅱ)求出BC所在直线的斜率,利用点斜式求BC所在直线的方程.
解答:解:(Ⅰ) 因为四边形OABC是矩形,OA所在直线的斜率为:KOA=
,
所以OC的斜率为:-
,OC所在直线方程为:y=-
x,
因为|OC|=|AB|=4,设点C的坐标(x,-
x),|OC|=
=2|x|=4,
解得x=2(舍)或x=-2;
所以所求C的坐标(-2,2
).
(Ⅱ)因为OA∥BC,所以BC 所在直线的斜率为
,又C(-2,2
),
所以BC所在直线的方程:y-2
=
(x+2).
即BC所在直线的方程:x-
y+8=0.
| ||
| 3 |
所以OC的斜率为:-
| 3 |
| 3 |
因为|OC|=|AB|=4,设点C的坐标(x,-
| 3 |
x2+(-
|
解得x=2(舍)或x=-2;
所以所求C的坐标(-2,2
| 3 |
(Ⅱ)因为OA∥BC,所以BC 所在直线的斜率为
| ||
| 3 |
| 3 |
所以BC所在直线的方程:y-2
| 3 |
| ||
| 3 |
即BC所在直线的方程:x-
| 3 |
点评:本题考查直线方程的求法,两点间距离公式的应用,点斜式方程的应用,考查计算能力.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
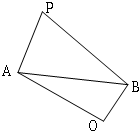 如图,已知四边形PAOB中,PA⊥OA,PB⊥OB.且PA=5,PB=8,AB=7
如图,已知四边形PAOB中,PA⊥OA,PB⊥OB.且PA=5,PB=8,AB=7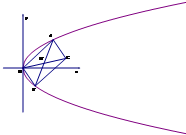 如图,已知抛物线P:y2=x,直线AB与抛物线P交于A,B两点,OA⊥OB,
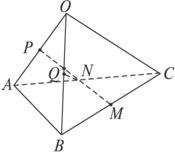
如图,已知抛物线P:y2=x,直线AB与抛物线P交于A,B两点,OA⊥OB, 如图,已知空间四边形OABC,其对角线为OB、AC,M、N分别是对边OA、BC的中点,点G在线段MN上,且
如图,已知空间四边形OABC,其对角线为OB、AC,M、N分别是对边OA、BC的中点,点G在线段MN上,且