题目内容
已知正方形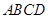 的边长为2,
的边长为2,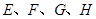 分别是边
分别是边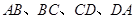 的中点.
的中点.
(1)在正方形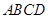 内部随机取一点
内部随机取一点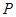 ,求满足
,求满足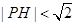 的概率;
的概率;
(2)从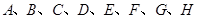 这八个点中,随机选取两个点,记这两个点之间的距离为
这八个点中,随机选取两个点,记这两个点之间的距离为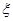 ,求随机变量
,求随机变量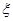 的分布列与数学期望
的分布列与数学期望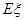 .
.
(1) ;(2)详见解析
;(2)详见解析
【解析】
试题分析:(1)首先判断这是一个几何概型,然后找出符合条件的区域与总区域的面积,利用面积之比即可算出相应的古典概型的概率;(2)先确定这八个点连线距离的几种情况,然后就不同的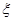 的值进行计算,利用离散型随机变量的计算方法列表并计算相应的数学期望。
的值进行计算,利用离散型随机变量的计算方法列表并计算相应的数学期望。
试题解析:(1)这是一个几何概型.所有点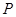 构成的平面区域是正方形
构成的平面区域是正方形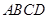 的内部,其面积是
的内部,其面积是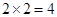 .
.
1分
满足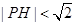 的点
的点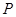 构成的平面区域是以
构成的平面区域是以 为圆心,
为圆心,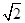 为半径的圆的内部与正方形
为半径的圆的内部与正方形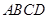 内部的公共部分,它可以看作是由一个以
内部的公共部分,它可以看作是由一个以 为圆心、
为圆心、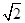 为半径、圆心角为
为半径、圆心角为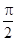 的扇形
的扇形 的内部(即四分之一个圆)与两个直角边为1的等腰直角三角形(△
的内部(即四分之一个圆)与两个直角边为1的等腰直角三角形(△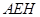 和△
和△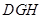 )内部构成.
2分
)内部构成.
2分

其面积是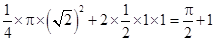 . 3分
. 3分
所以满足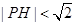 的概率为
的概率为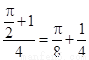 . 4分
. 4分
(2)从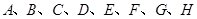 这八个点中,任意选取两个点,共可构成
这八个点中,任意选取两个点,共可构成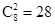 条不同的线段.
条不同的线段.
5分
其中长度为1的线段有8条,长度为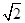 的线段有4条,长度为2的线段有6条,长度为
的线段有4条,长度为2的线段有6条,长度为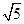 的线段有8条,长度为
的线段有8条,长度为 的线段有2条.
的线段有2条.
所以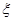 所有可能的取值为
所有可能的取值为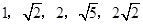 .
7分
.
7分
且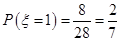 ,
,  ,
, 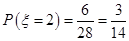 ,
,
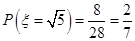 ,
, 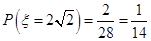 .
9分
.
9分
所以随机变量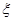 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10分
随机变量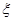 的数学期望为
的数学期望为
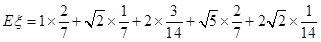
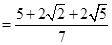 .
12分
.
12分
考点:几何概型、古典概型、排列组合、离散型随机变量的分布列与数学期望

| 2 |
| AB |
| a |
| BC |
| b |
| AC |
| c |
| a |
| b |
| c |
| A、0 | ||
B、
| ||
| C、2 | ||
| D、4 |






 如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.
如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标. 的边长为2,
的边长为2,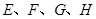 分别是边
分别是边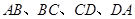 的中点.
的中点.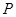 ,求满足
,求满足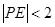 的概率;
的概率;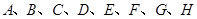 这八个点中,随机选取两个点,记这两个点之间的距离的平方为
这八个点中,随机选取两个点,记这两个点之间的距离的平方为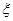 ,求
,求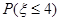 .
. 的边长为2,
的边长为2, .将正方形
.将正方形 折起,
折起, ,得到三棱锥
,得到三棱锥 ,如图所示.
,如图所示. 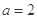 时,求证:
时,求证: ;
;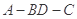 的大小为
的大小为 时,求二面角
时,求二面角 的正切值.
的正切值.