题目内容
已知二次函数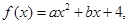 集合
集合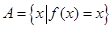
(1)若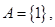 求函数
求函数 的解析式;
的解析式;
(2)若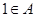 ,且
,且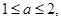 设
设 在区间
在区间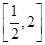 上的最大值、最小值分别为
上的最大值、最小值分别为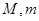 ,记
,记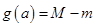 ,求
,求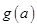 的最小值.
的最小值.
(1) (2)
(2)
解析试题分析:(1)由集合的意义可知 表示方程
表示方程 有两个相等的实数即二次方程的判别式为0.(2)这类题型熟练掌握二次函数的单调性和分类讨论思想方法是解题的关键,本题特殊在对称轴在区间内且离右端点近,所以不用分类讨论最值位置.求出最值得到
有两个相等的实数即二次方程的判别式为0.(2)这类题型熟练掌握二次函数的单调性和分类讨论思想方法是解题的关键,本题特殊在对称轴在区间内且离右端点近,所以不用分类讨论最值位置.求出最值得到 可由单调性其最小值.
可由单调性其最小值.
试题解析:
(1)由 知二次方程
知二次方程 有两个相等的实数根
有两个相等的实数根
故 解得:
解得: ,所以
,所以 (5分)
(5分)
(2)因为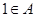 ,所以
,所以 ,又因为
,又因为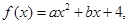
所以
 7分
7分
对称轴 因为
因为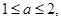 所以
所以 又因为
又因为 ,
,
所以 10分
10分 ,所以
,所以 ,在
,在 上为关于a的增函数,
上为关于a的增函数,
故当 时,
时, 12分
12分
考点:函数的图象;二次函数的性质;二次函数在闭区间上的最值

练习册系列答案
相关题目
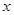 (百台),其总成本为
(百台),其总成本为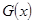 (万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本)。销售收入
(万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本)。销售收入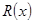 (万元)满足
(万元)满足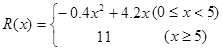 ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题: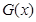 和利润函数
和利润函数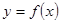 的解析式(利润=销售收入—总成本);
的解析式(利润=销售收入—总成本);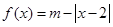 ,
,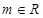 ,且
,且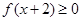 的解集为
的解集为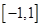 .
.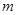 的值;
的值;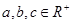 ,且
,且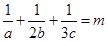 ,求证:
,求证: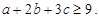
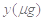 与服药后的时间
与服药后的时间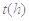 之间近似满足如图所示的曲线.其中
之间近似满足如图所示的曲线.其中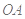 是线段,曲线段
是线段,曲线段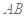 是函数
是函数
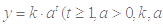 是常数
是常数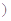 的图象.
的图象.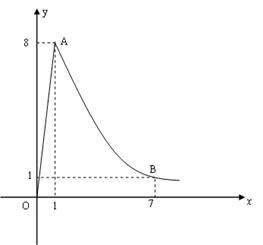
 关于时间
关于时间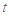 的函数关系式;
的函数关系式;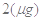 时治疗有效,假若某病人第一次服药为早上
时治疗有效,假若某病人第一次服药为早上 ,为保持疗效,第二次服药最迟是当天几点钟?
,为保持疗效,第二次服药最迟是当天几点钟?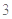
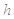 ,该病人每毫升血液中含药量为多少
,该病人每毫升血液中含药量为多少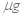 ?
?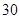 天内每件的销售价格
天内每件的销售价格 (元)与时间
(元)与时间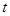 (天)的函数关系是
(天)的函数关系是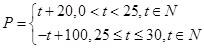 该商品的日销售量
该商品的日销售量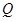 (件)与时间
(件)与时间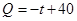
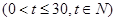 ,设商品的日销售额为
,设商品的日销售额为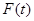 (销售量与价格之积)
(销售量与价格之积)
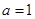 时,求函数
时,求函数 在
在 的值域;
的值域;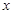 的方程
的方程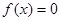 有解,求
有解,求 的取值范围.
的取值范围.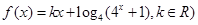 是偶函数.
是偶函数.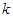 的值;
的值;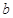 ,函数
,函数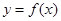 的图像与直线
的图像与直线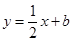 最多只有一个交点;
最多只有一个交点;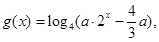 若函数
若函数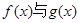 的图像有且只有一个公共点,求实数
的图像有且只有一个公共点,求实数 的取值范围.
的取值范围.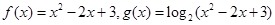 ,且两函数定义域均为
,且两函数定义域均为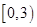 ,
, 在定义域内的图像,并求
在定义域内的图像,并求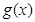 的值域.(5分)
的值域.(5分)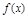 =x2-4x+a+3,g(x)=mx+5-2m.
=x2-4x+a+3,g(x)=mx+5-2m.