题目内容
两个边长均为3的正方形ABCD和ABEF所在平面垂直相交于AB,M∈AC,N∈FB,且AM=FN.
(1)证明:MN∥平面BCE;
(2)当AM=FN=
时,求MN的长度.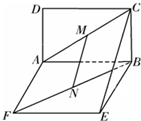
(1)证明:MN∥平面BCE;
(2)当AM=FN=
| 2 |

证明:(1)证法一:(线面平行的判定定理法)
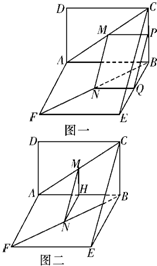
如图一,作MP⊥BC,NQ⊥BE,P、Q为垂足,连接PQ,
则MP∥AB,NQ∥AB.
所以MP∥NQ,
又AM=NF,AC=BF,
所以MC=NB.
又∠MCP=∠NBQ=45°,
所以Rt△MCP≌Rt△NBQ,
所以MP=NQ.
故四边形MPQN为平行四边形.
所以MN∥PQ.…..(4分)
因为PQ∥平面BCE,MN∥平面BCE,
所以MN∥平面BCE…..(6分)
法二:如图二,过M作MH⊥AB于H,则MH∥BC.
所以
=
.
连接NH,由BF=AC,FN=AM,得
=
,
所以NH∥AF∥BE.…..(2分)
又∵NH∩BH=H,BC∩BE=B,NH,BH?平面MNH,BC,BE?平面BCE
∴平面MNH∥平面BCE…..(4分)
因为MN?平面MNH,
所以MN∥平面BCE.…..(6分)
(2)如图二,∵AM=FN=
由比例关系易得:
∵
=
=
=
=
,
∴在Rt△ABC中,MH=1,
在Rt△ABF中,NH=2,
∴在Rt△MNH中,MN=
.…..(12分)
如图一,作MP⊥BC,NQ⊥BE,P、Q为垂足,连接PQ,
则MP∥AB,NQ∥AB.
所以MP∥NQ,
又AM=NF,AC=BF,
所以MC=NB.
又∠MCP=∠NBQ=45°,
所以Rt△MCP≌Rt△NBQ,
所以MP=NQ.
故四边形MPQN为平行四边形.
所以MN∥PQ.…..(4分)
因为PQ∥平面BCE,MN∥平面BCE,
所以MN∥平面BCE…..(6分)
法二:如图二,过M作MH⊥AB于H,则MH∥BC.

所以
| AM |
| AC |
| AH |
| AB |
连接NH,由BF=AC,FN=AM,得
| FN |
| FB |
| AH |
| AB |
所以NH∥AF∥BE.…..(2分)
又∵NH∩BH=H,BC∩BE=B,NH,BH?平面MNH,BC,BE?平面BCE
∴平面MNH∥平面BCE…..(4分)
因为MN?平面MNH,
所以MN∥平面BCE.…..(6分)
(2)如图二,∵AM=FN=
| 2 |
由比例关系易得:
∵
| AM |
| AC |
| FN |
| FB |
| AH |
| AB |
| MH |
| BC |
| 1 |
| 3 |
∴在Rt△ABC中,MH=1,
在Rt△ABF中,NH=2,
∴在Rt△MNH中,MN=
| 5 |

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
如图所示,在平面直角坐标系xOy上放置一个边长为1的正方形PABC,此正方形PABC沿x轴滚动(向左或向右均可),滚动开始时,点P位于原点处,设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),x∈R,该函数相邻两个零点之间的距离为m.
(1)写出m的值并求出当0≤x≤m时,点P运动路径的长度l;
(2)写出函数f(x),x∈[4k-2,4k+2],k∈Z的表达式;研究该函数的性质并填写下面表格:
(3)试讨论方程f(x)=a|x|在区间[-8,8]上根的个数及相应实数a的取值范围.

(1)写出m的值并求出当0≤x≤m时,点P运动路径的长度l;
(2)写出函数f(x),x∈[4k-2,4k+2],k∈Z的表达式;研究该函数的性质并填写下面表格:
| 函数性质 | 结 论 | |
| 奇偶性 | ______ | |
| 单调性 | 递增区间 | ______ |
| 递减区间 | ______ | |
| 零点 | ______ | |

 如图,将边长为3的正方形ABCD绕中心O顺时针旋转α (0<α<
如图,将边长为3的正方形ABCD绕中心O顺时针旋转α (0<α<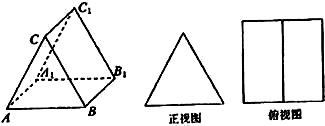 如图,三棱柱的侧棱长和底面边长均为2,且侧棱AA1⊥平面A1B1C1,它的正视图是等边三角形,俯视图是由两个全等的矩形组成的正方形,该三棱柱的侧视图面积为( )
如图,三棱柱的侧棱长和底面边长均为2,且侧棱AA1⊥平面A1B1C1,它的正视图是等边三角形,俯视图是由两个全等的矩形组成的正方形,该三棱柱的侧视图面积为( ) (2012•浦东新区一模)如图所示,在平面直角坐标系xOy上放置一个边长为1的正方形PABC,此正方形PABC沿x轴滚动(向左或向右均可),滚动开始时,点P位于原点处,设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),x∈R,该函数相邻两个零点之间的距离为m.
(2012•浦东新区一模)如图所示,在平面直角坐标系xOy上放置一个边长为1的正方形PABC,此正方形PABC沿x轴滚动(向左或向右均可),滚动开始时,点P位于原点处,设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),x∈R,该函数相邻两个零点之间的距离为m. 如图,将边长为3的正方形ABCD绕中心O顺时针旋转α (0<α<
如图,将边长为3的正方形ABCD绕中心O顺时针旋转α (0<α< )得到正方形A′B′C′D′.根据平面几何知识,有以下两个结论:
)得到正方形A′B′C′D′.根据平面几何知识,有以下两个结论: