题目内容
 如图,将边长为3的正方形ABCD绕中心O顺时针旋转α (0<α<
如图,将边长为3的正方形ABCD绕中心O顺时针旋转α (0<α<| π |
| 2 |
①∠A′FE=α;
②对任意α (0<α<
| π |
| 2 |
(1)设A′E=x,将x表示为α的函数;
(2)试确定α,使正方形A′B′C′D′与正方形ABCD重叠部分面积最小,并求最小面积.
分析:(1)利用AB=AE+EF+BF=3,表示出相应线段长,即可将x表示为α的函数;
(2)求正方形A′B′C′D′与正方形ABCD重叠部分面积最小,即求S△A′EF的最大值,表示出S△A′EF,利用换元法,即可求得面积的最大值,从而可得结论.
(2)求正方形A′B′C′D′与正方形ABCD重叠部分面积最小,即求S△A′EF的最大值,表示出S△A′EF,利用换元法,即可求得面积的最大值,从而可得结论.
解答: 解:(1)在Rt△EA′F中,因为∠A′FE=α,A′E=x,
解:(1)在Rt△EA′F中,因为∠A′FE=α,A′E=x,
所以EF=
,A′F=
.
由题意AE=A′E=x,BF=A′F=
,
所以AB=AE+EF+BF=x+
+
=3.
所以x=
,α∈(0,
) …(6分)
(2)S△A′EF=
•A′E•A′F=
•x•
=
=(
)2•
=
. …(10分)
令t=sinα+cosα,则sinαcosα=
.
因为α∈(0,
),所以α+
∈(
,
),所以t=
sin(α+
)∈(1,
].
S△A′EF=
=
(1-
)≤
(1-
).
正方形A′B′C′D′与正方形ABCD重叠部分面积S=S正方形A′B′C′D′-4S△A′EF≥9-9 (1-
)=18(
-1).
当t=
,即α=
时等号成立. …(15分)
答:当α=
时,正方形A′B′C′D′与正方形ABCD重叠部分面积最小,最小值为18(
-1).…(16分)
 解:(1)在Rt△EA′F中,因为∠A′FE=α,A′E=x,
解:(1)在Rt△EA′F中,因为∠A′FE=α,A′E=x,所以EF=
| x |
| sinα |
| x |
| tanα |
由题意AE=A′E=x,BF=A′F=
| x |
| tanα |
所以AB=AE+EF+BF=x+
| x |
| sinα |
| x |
| tanα |
所以x=
| 3sinα |
| 1+sinα+cosα |
| π |
| 2 |
(2)S△A′EF=
| 1 |
| 2 |
| 1 |
| 2 |
| x |
| tanα |
| x2 |
| 2tanα |
=(
| 3sinα |
| 1+sinα+cosα |
| cosα |
| 2sinα |
| 9sinαcosα |
| 2(1+sinα+cosα)2 |
令t=sinα+cosα,则sinαcosα=
| t2-1 |
| 2 |
因为α∈(0,
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| 2 |
| π |
| 4 |
| 2 |
S△A′EF=
| 9(t2-1) |
| 4(1+t)2 |
| 9 |
| 4 |
| 2 |
| t+1 |
| 9 |
| 4 |
| 2 | ||
|
正方形A′B′C′D′与正方形ABCD重叠部分面积S=S正方形A′B′C′D′-4S△A′EF≥9-9 (1-
| 2 | ||
|
| 2 |
当t=
| 2 |
| π |
| 4 |
答:当α=
| π |
| 4 |
| 2 |
点评:本题考查函数模型的构建,考查面积的计算,考查换元法,考查学生利用数学知识解决实际问题,属于中档题.

练习册系列答案
相关题目
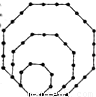
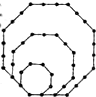 (2012•芜湖三模)如图,将边长为1,2,3的正八边形叠放在一起,同一边上相邻珠子的距离为1,若以此方式再放置边长为4,5,6,…,10的正八边形,则这10个正八边形镶嵌的珠子总数是
(2012•芜湖三模)如图,将边长为1,2,3的正八边形叠放在一起,同一边上相邻珠子的距离为1,若以此方式再放置边长为4,5,6,…,10的正八边形,则这10个正八边形镶嵌的珠子总数是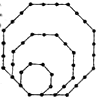 如图,将边长为1,2,3的正八边形叠放在一起,同一边上相邻珠子的距离为1,若以此方式再放置边长为4,5,6,…,10的正八边形,则这10个正八边形镶嵌的珠子总数是________.
如图,将边长为1,2,3的正八边形叠放在一起,同一边上相邻珠子的距离为1,若以此方式再放置边长为4,5,6,…,10的正八边形,则这10个正八边形镶嵌的珠子总数是________.