题目内容
2.已知函数f(x)=x2+2ax+2.(1)若函数f(x)有两个不相等的正零点,求a的取值范围;
(2)若函数f(x)在x∈[-5,5]上的最小值为-3,求a的值.
分析 (1)利用二次函数的性质,列出不等式组求解即可.
(2)利用二次函数的闭区间上的最值,列出不等式组,求解即可.
解答 解:(1)函数f(x)=x2+2ax+2.恒过(0,2),函数f(x)有两个不相等的正零点,
可得$\left\{\begin{array}{l}△>0\\-a>0\end{array}\right.$,即$\left\{\begin{array}{l}{4{a}^{2}-8>0}\\{-a>0}\end{array}\right.$,所以a<-$\sqrt{2}$.
(2)函数f(x)=x2+2ax+2,的对称轴为:x=-a,-a<-5时,f(-5)是函数的最小值:27-10a;
-a∈[-5,5]时,f(-a)是最小值:2-a2;当-a>5时,f(5)是函数的最小值:27+10a,
因为在x∈[-5,5]上的最小值为-3,
$f{\;}_{min}(x)=\left\{\begin{array}{l}27-10a({a>5})\\ 2-{a^2}({-5≤a≤5})\\ 27+10a({a<-5})\end{array}\right.$,
当a>5时,27-10a=-3,解得a=3舍去;
当a<-5时,27+10a=-3,解得a=-3舍去.
当$\left\{\begin{array}{l}2-{a^2}=-3\\-5≤a≤5\end{array}\right.$时有解,$a=±\sqrt{5}$.
所求a为:$±\sqrt{5}$.
点评 本题考查二次函数的简单性质的应用,函数的最值的求法,考查转化思想以及计算能力.

练习册系列答案
相关题目
12.复数$z=\frac{i+1}{{-{i^2}-3i}}$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14.如果圆(x-a)2+(y-a)2=8上存在一点P到直线y=-x的最短距离为$\sqrt{2}$,则实数a的值为( )
| A. | -3 | B. | 3 | C. | $3\sqrt{2}$ | D. | -3或3 |
11.已知双曲线E:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,|F1F2|=6,P是E右支上一点,PF1与y轴交于点A,△PAF2的内切圆在边AF2上的切点为Q,若|AQ|=$\sqrt{3}$,则E的离心率是( )
| A. | 2$\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
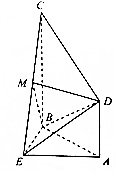 如图,在多面体ABCDE中,平面ABE⊥平面ABCD,△ABE是等边三角形,四边形ABCD是直角梯形,AB⊥AD,AB⊥BC,AB=AD=$\frac{1}{2}$BC=2,M是EC的中点.
如图,在多面体ABCDE中,平面ABE⊥平面ABCD,△ABE是等边三角形,四边形ABCD是直角梯形,AB⊥AD,AB⊥BC,AB=AD=$\frac{1}{2}$BC=2,M是EC的中点.