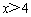题目内容
已知抛物线 的顶点在坐标原点
的顶点在坐标原点 ,对称轴为
,对称轴为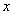 轴,焦点为
轴,焦点为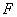 ,抛物线上一点
,抛物线上一点 的横坐标为2,且
的横坐标为2,且 .
.
(Ⅰ)求抛物线的方程;
(Ⅱ)过点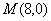 作直线
作直线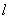 交抛物线于
交抛物线于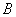 ,
,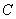 两点,求证:
两点,求证: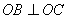 .
.
解:(Ⅰ)由题设抛物线的方程为: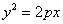
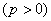 ,
,
则点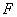 的坐标为
的坐标为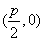 ,点
,点 的一个坐标为
的一个坐标为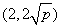 ,
,
∵ ,∴
,∴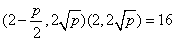 ,
,
∴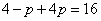 ,∴
,∴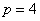 ,∴
,∴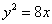 .
.
(Ⅱ)设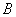 、
、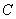 两点坐标分别为
两点坐标分别为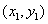 、
、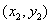 ,
,
法一:因为直线当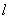 的斜率不为0,设直线当
的斜率不为0,设直线当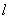 的方程为
的方程为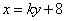
方程组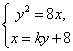 得
得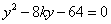 ,
,
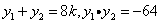
因为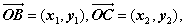
所以
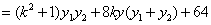 =0,
=0,
所以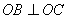 .
.
法二:①当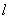 的斜率不存在时,
的斜率不存在时,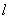 的方程为
的方程为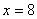 ,此时
,此时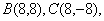
即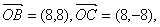 有
有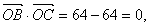 所以
所以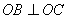 .
.
② 当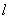 的斜率存在时,设
的斜率存在时,设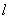 的方程为
的方程为
方程组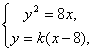 得
得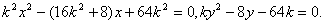
所以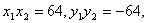 因为
因为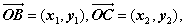
所以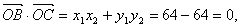
所以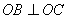 .
.
由①②得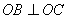 .
.

练习册系列答案
相关题目
 为增函数的区间是 。
为增函数的区间是 。 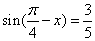 ,则sin
,则sin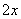 的值为 .
的值为 .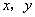 满足
满足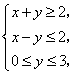 则
则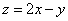 的最小值是( )
的最小值是( )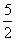 (C)
(C) (D)
(D)
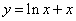 在点(1,1)处的切线方程为 .
在点(1,1)处的切线方程为 .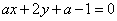 与直线
与直线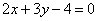 垂直,则
垂直,则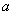 的值为 ( )
的值为 ( ) 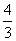 D.
D.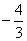
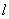 为直线,
为直线,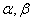 是两个不同的平面,下列命题中正确的是 ( )
是两个不同的平面,下列命题中正确的是 ( )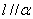 ,
,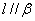 ,则
,则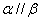 B.若
B.若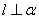 ,
,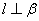 ,则
,则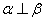 ,
,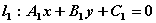 ,
,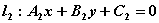 垂直的充要条件是
垂直的充要条件是 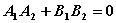 B、
B、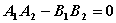 C、
C、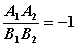 D、
D、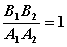
 B.
B.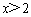
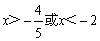 D.
D.