题目内容
已知实数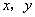 满足
满足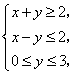 则
则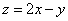 的最小值是( )
的最小值是( )
(A)5 (B)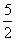 (C)
(C) (D)
(D)
C

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
题目内容
已知实数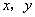 满足
满足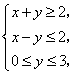 则
则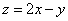 的最小值是( )
的最小值是( )
(A)5 (B)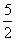 (C)
(C) (D)
(D)
C

 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案