题目内容
14.设直线ax-y+3=0与圆(x-1)2+(y-2)2=4有两个不同的交点A,B,且弦AB的长为2$\sqrt{3}$,则a等于0.分析 先确定圆心和半径,然后利用圆中的垂径定理求得圆心到直线的距离,从而建立关于a的方程,即可求得a的值.
解答 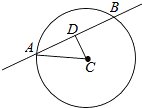 解:圆(x-1)2+(y-2)2=4的圆心C(1,2),半径r=2
解:圆(x-1)2+(y-2)2=4的圆心C(1,2),半径r=2
弦AB的中点为D,则|AD|=$\sqrt{3}$,由圆的性质得圆心到直线的距离d=1,
∴C到直线的距离为$\frac{|a-2+3|}{\sqrt{{a}^{2}+1}}$=1
即|a+1|=$\sqrt{{a}^{2}+1}$,
平方得a2+2a+1=a2+1,
即2a=0,
解得:a=0,
故答案为:0.
点评 本题考查了直线与圆相交的性质,注意圆中的直角三角形的应用,避免联立直线与圆的方程,利用半径,半弦,圆心距之间的关系是解决本题的关键.

练习册系列答案
相关题目
6.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别F1(-c,0),F2(c,0),若双曲线上存在点P满足$\frac{a}{sin∠PF{{\;}_{1}F}_{2}}$=$\frac{c}{sin∠P{F}_{2}{F}_{1}}$1,则该曲线的离心率的取值范围为( )
| A. | (1,$\sqrt{2}$+1) | B. | (1,$\sqrt{3}$) | C. | ($\sqrt{3}$,+∞) | D. | ($\sqrt{2}$+1,+∞) |
3.下列函数既是奇函数,又在区间[-1,1]上单调递增的是( )
| A. | y=sin2x | B. | y=-|x+1| | C. | y=ln$\frac{2+x}{2-x}$ | D. | y=$\frac{{a}^{x}+{a}^{-x}}{2}$ |
 函数y=Asin(ωx+φ)+k在一个周期内的图象如图所示,且ω>0,求其解析式.
函数y=Asin(ωx+φ)+k在一个周期内的图象如图所示,且ω>0,求其解析式.