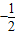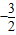题目内容
如图,在等腰直角△ABC中,点D是斜边BC的中点,过点D的直线分别交AB,AC于点M,N,若
=x
,
=y
,其中x>0,y>0,则2x+4y的最小值是______.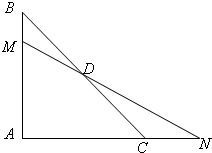
| AM |
| AB |
| AN |
| AC |

以AC、AB为a,b轴建立直角坐标系,设等腰直角△ABC的腰长为2,
则D点坐标为(1,1),B(0,2)、C(2,0),
∵
=x
,
=y
,
∴点M坐标为(0,2x),点N的坐标为(2y,0)
∴直线MN的方程为
+
=1
∵直线MN过点D(1,1),
∴
+
=1
∴
+
=2
则2x+4y=(
+
)x+2?(
+
)y=3+(
+
)≥3+2
故答案为:3+2
则D点坐标为(1,1),B(0,2)、C(2,0),
∵
| AM |
| AB |
| AN |
| AC |
∴点M坐标为(0,2x),点N的坐标为(2y,0)
∴直线MN的方程为
| a |
| 2x |
| b |
| 2y |
∵直线MN过点D(1,1),
∴
| 1 |
| 2x |
| 1 |
| 2y |
∴
| 1 |
| x |
| 1 |
| y |
则2x+4y=(
| 1 |
| x |
| 1 |
| y |
| 1 |
| x |
| 1 |
| y |
| x |
| y |
| 2y |
| x |
| 2 |
故答案为:3+2
| 2 |

练习册系列答案
相关题目
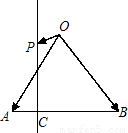
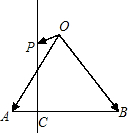 如图,在等腰直角△ABO中,设
如图,在等腰直角△ABO中,设 如图,在等腰直角三角形ABC中,则AM<AC的概率为( )
如图,在等腰直角三角形ABC中,则AM<AC的概率为( ) 为AB上靠近点A的四等分点,过C作AB的垂线L,设P为垂线上任一点,
为AB上靠近点A的四等分点,过C作AB的垂线L,设P为垂线上任一点,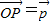 ,则
,则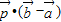 =( )
=( )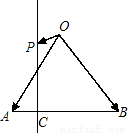
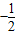



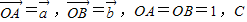 为AB上靠近点A的四等分点,过C作AB的垂线L,设P为垂线上任一点,
为AB上靠近点A的四等分点,过C作AB的垂线L,设P为垂线上任一点,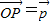 ,则
,则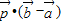 =( )
=( )
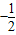

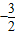

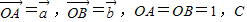 为AB上靠近点A的四等分点,过C作AB的垂线L,设P为垂线上任一点,
为AB上靠近点A的四等分点,过C作AB的垂线L,设P为垂线上任一点,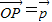 ,则
,则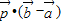 =( )
=( )