题目内容
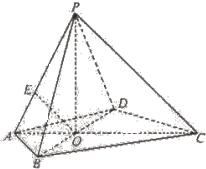 如图,在四边形ABCD中,AC⊥BD,垂足为O,PO⊥平面ABCD,AO=BO=DO=1,CO=PO=2,E是线段PA上的点,AE:AP=1:3.
如图,在四边形ABCD中,AC⊥BD,垂足为O,PO⊥平面ABCD,AO=BO=DO=1,CO=PO=2,E是线段PA上的点,AE:AP=1:3.(1)求证:OE∥平面PBC;
(2)求二面角D-PB-C的大小.
分析:对于(1),要证明OE∥平面PBC,只需证明OE与平面PBC内的一条直线平行即可,而AO=BO=DO=1,CO=PO=2,
AE:AP=1:3,可以确定O是AC的三等分点,从而可以证明OE∥PC,从而得证;
对于(2),由AC⊥BD,垂足为O,PO⊥平面ABCD,可以得到OA、OB、OC三条线两两垂直,且二面角D-PB-C的平面角为锐角,
因而可以建立空间直角坐标系,将求二面角问题转化为求平面PBC与平面PBD的法向量的夹角.
AE:AP=1:3,可以确定O是AC的三等分点,从而可以证明OE∥PC,从而得证;
对于(2),由AC⊥BD,垂足为O,PO⊥平面ABCD,可以得到OA、OB、OC三条线两两垂直,且二面角D-PB-C的平面角为锐角,
因而可以建立空间直角坐标系,将求二面角问题转化为求平面PBC与平面PBD的法向量的夹角.
解答: 证明:(1)由题意AE:AP=1:3,
证明:(1)由题意AE:AP=1:3,
又AO=1,AC=3,
∴AO:AC=1:3,
三角形PAC中,有OE∥PC,
又OE?平面PBC,PC?平面PBC,
由线面平行的判定定理得:OE∥平面PBC;
(2)解:如图,建立空间直角坐标系O-xyz,由已知可得个点坐标:B(1,0,0),C(0,2,0),
P(0,0,2),D(-1,0,0)∴
=(1,0,-2),
=(0,,2,-2),
设平面PBC的一个法向量为:
=(x,y,z),则
解得:
,
取x=2,y=1,z=1,得:
=(2,1,1);
取平面PBD的一个法向量为
═(0,1,0),则cos<
,
>=
=
=
,
又因为二面角D-PB-C的平面角为锐角,所以二面角D-PB-C的大小为arcos
.
 证明:(1)由题意AE:AP=1:3,
证明:(1)由题意AE:AP=1:3,又AO=1,AC=3,
∴AO:AC=1:3,
三角形PAC中,有OE∥PC,
又OE?平面PBC,PC?平面PBC,
由线面平行的判定定理得:OE∥平面PBC;
(2)解:如图,建立空间直角坐标系O-xyz,由已知可得个点坐标:B(1,0,0),C(0,2,0),
P(0,0,2),D(-1,0,0)∴
| PB |
| PC |
设平面PBC的一个法向量为:
| n |
|
|
取x=2,y=1,z=1,得:
| n |
取平面PBD的一个法向量为
| m |
| m |
| n |
| ||||
|
| 1 | ||
|
| ||
| 6 |
又因为二面角D-PB-C的平面角为锐角,所以二面角D-PB-C的大小为arcos
| ||
| 6 |
点评:本题考查线面平行的判定和二面角的求法,注意其中转化思想的应用,将线面平行转化为线线平行,将二面角转化为向量的夹角去求.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
 如图,在四边形ABCD中,△ABC为边长等于
如图,在四边形ABCD中,△ABC为边长等于 如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=7,AD=6,S△ADC=
如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=7,AD=6,S△ADC= 如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=6,AD=5,S△ADC=
如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=6,AD=5,S△ADC=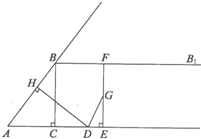 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BBl∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BBl∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒. (2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,
(2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,