题目内容
 已知圆内接△ABC中,D为BC上一点,且△ADC为正三角形,点E为BC的延长线上一点,AE为圆O的切线.
已知圆内接△ABC中,D为BC上一点,且△ADC为正三角形,点E为BC的延长线上一点,AE为圆O的切线.(Ⅰ)求∠BAE 的度数;
(Ⅱ)求证:CD2=BD•EC.
考点:相似三角形的判定
专题:选作题,立体几何
分析:(Ⅰ)证明∠EBA=∠EAC,可得∠EAB=∠ECA,利用△ADC为正三角形,即可求∠BAE 的度数;
(Ⅱ)先证明△ABD∽△EAC,可得AD•CA=BD•EC,再结合△ACD为等边三角形,所以AD=AC=CD,即可得出结论
(Ⅱ)先证明△ABD∽△EAC,可得AD•CA=BD•EC,再结合△ACD为等边三角形,所以AD=AC=CD,即可得出结论
解答:
证明:(Ⅰ)在△EAB与△ECA中,
因为AE为圆O的切线,
所以∠EBA=∠EAC
因为∠E公用,
所以∠EAB=∠ECA,
因为△ADC为正三角形,
所以∠BAE=∠ECA=120°;
(Ⅱ)因为AE为圆O的切线,所以∠ABD=∠CAE.
因为△ACD为等边三角形,所以∠ADC=∠ACD,
所以∠ADB=∠ECA,所以△ABD∽△EAC.
所以
=
,即AD•CA=BD•EC.
因为△ACD为等边三角形,所以AD=AC=CD,
所以CD2=BD•EC.
因为AE为圆O的切线,
所以∠EBA=∠EAC
因为∠E公用,
所以∠EAB=∠ECA,
因为△ADC为正三角形,
所以∠BAE=∠ECA=120°;
(Ⅱ)因为AE为圆O的切线,所以∠ABD=∠CAE.
因为△ACD为等边三角形,所以∠ADC=∠ACD,
所以∠ADB=∠ECA,所以△ABD∽△EAC.
所以
| AD |
| BD |
| EC |
| CA |
因为△ACD为等边三角形,所以AD=AC=CD,
所以CD2=BD•EC.
点评:本题考查三角形相似的判断,考查圆的切线的性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
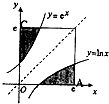 如图,在边长为e(e为自然对数的底数)的正方形区域的A处于C处各有一个通信基站,其信号覆盖范围分别为如图所示的阴影区域.该正方形区域内无其它信号来源且这两个基站工作正常,若在该正方形区域内随机选择一个地点,则该地点无信号的概率为( )
如图,在边长为e(e为自然对数的底数)的正方形区域的A处于C处各有一个通信基站,其信号覆盖范围分别为如图所示的阴影区域.该正方形区域内无其它信号来源且这两个基站工作正常,若在该正方形区域内随机选择一个地点,则该地点无信号的概率为( )A、
| ||
B、1-
| ||
C、
| ||
D、1-
|
设等差数列{an}的公差为d,且a3=2,若数列{2 a1an}为递增数列,则公差d的取值范围是( )
| A、d<0 | B、d>1 |
| C、d>1或d<0 | D、0<d<1 |
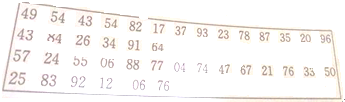 福利彩票“双色球”中,红球号码有编号为01,02,…,33的33个个体组成,某彩民利用下面的随机数表选取6组数作为6个红球的编号,选取方法是从随机数表第1行的第6列和第7列数字开始由左到右依次选取两个数字,则选出来的第6个红球的编号为( )
福利彩票“双色球”中,红球号码有编号为01,02,…,33的33个个体组成,某彩民利用下面的随机数表选取6组数作为6个红球的编号,选取方法是从随机数表第1行的第6列和第7列数字开始由左到右依次选取两个数字,则选出来的第6个红球的编号为( )| A、23 | B、09 | C、02 | D、17 |
已知等差数列{an}的公差为d(d>0),a1=1,S5=35,则d的值为( )
| A、3 | B、-3 | C、2 | D、4 |

