题目内容
已知函数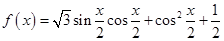 (1)求
(1)求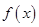 的单调减区间;(2)在锐角三角形ABC中,A、B、C的对边
的单调减区间;(2)在锐角三角形ABC中,A、B、C的对边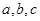 且满足
且满足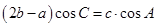 ,求
,求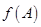 的取值范围.
的取值范围.
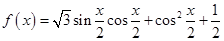 (1)求
(1)求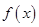 的单调减区间;(2)在锐角三角形ABC中,A、B、C的对边
的单调减区间;(2)在锐角三角形ABC中,A、B、C的对边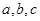 且满足
且满足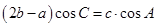 ,求
,求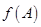 的取值范围.
的取值范围.(1)

 ;(2)
;(2)


 ;(2)
;(2)
试题分析:(1)求函数的单调区间需将已知化为
 的形式,然后利用复合函数的单调性处理,先逆用正弦的二倍角公式和降幂公式,然后利用辅助角公式即可求;(2)三角形问题中,如果有边角混合的式子,可考虑边角转化,或变为关于角的三角关系式,或变为关于边的代数式处理,该题先利用正弦定理把边化角,得三角关系式,从中解
的形式,然后利用复合函数的单调性处理,先逆用正弦的二倍角公式和降幂公式,然后利用辅助角公式即可求;(2)三角形问题中,如果有边角混合的式子,可考虑边角转化,或变为关于角的三角关系式,或变为关于边的代数式处理,该题先利用正弦定理把边化角,得三角关系式,从中解 ,然后结合已知条件得
,然后结合已知条件得 的范围(注意
的范围(注意 是锐角三角形这个条件),然后确定
是锐角三角形这个条件),然后确定 的范围,再结合
的范围,再结合 的图象求
的图象求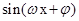 的范围,从而可求出
的范围,从而可求出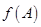 的取值范围.
的取值范围.试题解析:(1)由
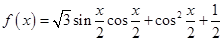 得
得 =
=
 ,∴
,∴ ,解得
,解得 ,
,故
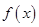 的单调减区间为
的单调减区间为

 ;
;(2)因为
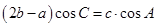 ,由正弦定理得
,由正弦定理得

 ,化简为
,化简为 ,所以
,所以
 =
= ,∴
,∴ =
= ,又因为
,又因为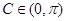 ,所以
,所以 ,由
,由 是锐角三角形,所以
是锐角三角形,所以 ,
, 

 ,
, ,∴
,∴ ,∴
,∴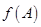 的取值范围.为
的取值范围.为 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
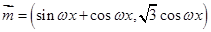 ,
,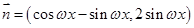 ,其中
,其中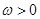 ,若函数
,若函数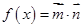 ,且函数
,且函数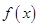 的图象与直线y=2两相邻公共点间的距离为
的图象与直线y=2两相邻公共点间的距离为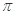 .
.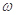 的值;
的值;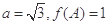 ,求△ABC周长的取值范围.
,求△ABC周长的取值范围. (其中
(其中 ),
), 、
、 是函数
是函数 的两个不同的零点,且
的两个不同的零点,且 的最小值为
的最小值为 .
. 的值;
的值; ,求
,求 的值.
的值. 中,
中,
 的取值范围.
的取值范围.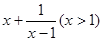 取得最小值a时,此时x的值为b,则
取得最小值a时,此时x的值为b,则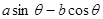 取得最大值时,
取得最大值时,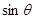 的值等于________。
的值等于________。 ,若
,若 ,且
,且 ,则
,则 的最小值为( )
的最小值为( )



 有两个不同的零点
有两个不同的零点 ,方程
,方程 有两个不同的实根
有两个不同的实根 .若这四个数按从小到大排列构成等差数列,则实数
.若这四个数按从小到大排列构成等差数列,则实数 的值为( )
的值为( )



 .
.