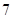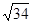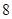题目内容
在△ABC中,内角A,B,C满足4sinAsinC-2cos(A-C)=1.
(Ⅰ)求角B的大小;
(Ⅱ)求sinA+2sinC的取值范围.
(Ⅰ)求角B的大小;
(Ⅱ)求sinA+2sinC的取值范围.
(Ⅰ)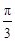 ;(Ⅱ)(
;(Ⅱ)(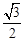 ,
,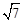 ].
].
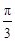 ;(Ⅱ)(
;(Ⅱ)(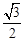 ,
,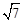 ].
].试题分析:(Ⅰ)先利用三角函数的和差化积公式化简等式,求得角B的余弦值,从而求得角B的大小;(Ⅱ)根据(Ⅰ)中角B的大小,把
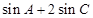 化为一个角的三角函数式,再根据此角的范围,求出整个式子的范围.
化为一个角的三角函数式,再根据此角的范围,求出整个式子的范围.试题解析:(Ⅰ)因为4sinAsinC-2cos(A-C)=4sinAsinC-2cosAcosC+2sinAsinC
=-2(cosAcosC-sinAsinC),
所以-2cos(A+C)=1,故cos B=
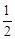 .
.又0<B<π,所以B=
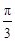 . 6分
. 6分(Ⅱ)由(Ⅰ)知C=
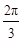 -A,故sinA+2sinC=2sinA+
-A,故sinA+2sinC=2sinA+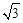 cosA=
cosA=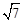 sin(A+θ),
sin(A+θ),其中0<θ<
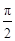 ,且sinθ=
,且sinθ=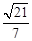 ,cosθ=
,cosθ=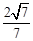 .
.由0<A<
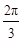 知,θ<A+θ<
知,θ<A+θ<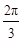 +θ,故
+θ,故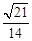 <sin(A+θ)≤1.
<sin(A+θ)≤1.所以sinA+2sinC∈(
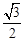 ,
,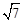 ]. 14分
]. 14分
练习册系列答案
相关题目
 .
. 的值;
的值; 的值.
的值.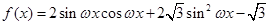 (
(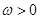 )的最小正周期为
)的最小正周期为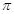 .求函数
.求函数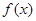 的单调增区间;
的单调增区间;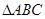 中,角
中,角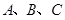 对边分别是
对边分别是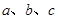 ,且满足
,且满足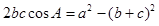 .若
.若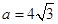 ,
,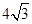 .求角
.求角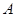 的大小和边b的长.
的大小和边b的长.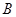 为钝角的的三角形
为钝角的的三角形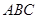 内角
内角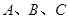 的对边分别为
的对边分别为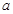 、
、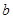 、
、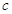 ,
,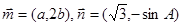 ,且
,且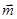 与
与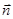 垂直.
垂直.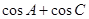 的取值范围
的取值范围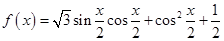 (1)求
(1)求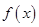 的单调减区间;(2)在锐角三角形ABC中,A、B、C的对边
的单调减区间;(2)在锐角三角形ABC中,A、B、C的对边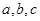 且满足
且满足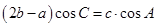 ,求
,求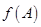 的取值范围.
的取值范围. .
.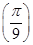 的值;
的值; ,若f
,若f =2,求cos
=2,求cos 的值.
的值.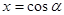 ,
,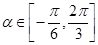 ,则
,则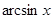 的取值范围为___________.
的取值范围为___________.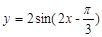 的图象关于点P
的图象关于点P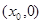 成中心对称,若
成中心对称,若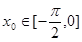 ,则
,则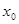 =________.
=________.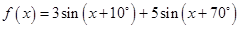 的最大值是( )
的最大值是( )