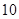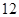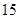题目内容
如果项数均为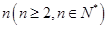 的两个数列
的两个数列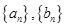 满足
满足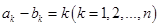 且集合
且集合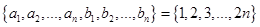 ,则称数列
,则称数列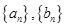 是一对“
是一对“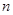 项相关数列”.
项相关数列”.
(Ⅰ)设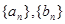 是一对“4项相关数列”,求
是一对“4项相关数列”,求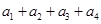 和
和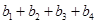 的值,并写出一对“
的值,并写出一对“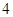 项相
项相
关数列”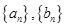 ;
;
(Ⅱ)是否存在“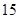 项相关数列”
项相关数列”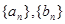 ?若存在,试写出一对
?若存在,试写出一对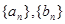 ;若不存在,请说明理由;
;若不存在,请说明理由;
(Ⅲ)对于确定的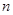 ,若存在“
,若存在“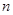 项相关数列”,试证明符合条件的“
项相关数列”,试证明符合条件的“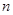 项相关数列”有偶数对.
项相关数列”有偶数对.
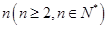 的两个数列
的两个数列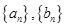 满足
满足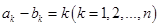 且集合
且集合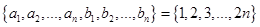 ,则称数列
,则称数列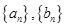 是一对“
是一对“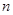 项相关数列”.
项相关数列”.(Ⅰ)设
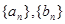 是一对“4项相关数列”,求
是一对“4项相关数列”,求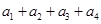 和
和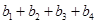 的值,并写出一对“
的值,并写出一对“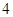 项相
项相关数列”
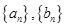 ;
;(Ⅱ)是否存在“
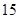 项相关数列”
项相关数列”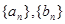 ?若存在,试写出一对
?若存在,试写出一对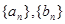 ;若不存在,请说明理由;
;若不存在,请说明理由;(Ⅲ)对于确定的
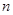 ,若存在“
,若存在“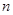 项相关数列”,试证明符合条件的“
项相关数列”,试证明符合条件的“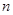 项相关数列”有偶数对.
项相关数列”有偶数对.(Ⅰ)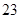 ;
;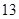 ;
;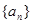 :8,4,6,5;
:8,4,6,5;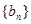 :7,2,3,1;(Ⅱ)不存在,理由见解析;(Ⅲ)证明见解析.
:7,2,3,1;(Ⅱ)不存在,理由见解析;(Ⅲ)证明见解析.
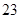 ;
;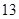 ;
;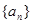 :8,4,6,5;
:8,4,6,5;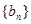 :7,2,3,1;(Ⅱ)不存在,理由见解析;(Ⅲ)证明见解析.
:7,2,3,1;(Ⅱ)不存在,理由见解析;(Ⅲ)证明见解析.试题分析:(Ⅰ)依题意有,
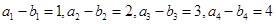 ,以及
,以及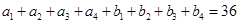 ,求得
,求得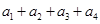 以及
以及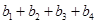 的值,写出符合条件的数列即可,答案不唯一;(Ⅱ)先假设存在,利用反证法证明得出矛盾,即可证明满足已知条件的“10项相关数列”不存在.依题意有
的值,写出符合条件的数列即可,答案不唯一;(Ⅱ)先假设存在,利用反证法证明得出矛盾,即可证明满足已知条件的“10项相关数列”不存在.依题意有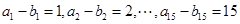 ,以及
,以及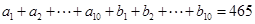 成立,解出
成立,解出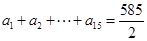 与已知矛盾,即证;(Ⅲ)对于确定的
与已知矛盾,即证;(Ⅲ)对于确定的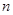 ,任取一对“
,任取一对“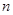 项相关数列”
项相关数列”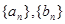 ,构造新数对
,构造新数对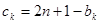 ,
,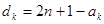
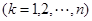 ,则可证明新数对也是“
,则可证明新数对也是“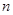 项相关数列”,但是数列
项相关数列”,但是数列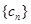 与
与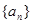 是不同的数列,可知“
是不同的数列,可知“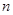 项相关数列”都是成对对应出现的,即符合条件的 “
项相关数列”都是成对对应出现的,即符合条件的 “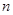 项相关数列”有偶数对.
项相关数列”有偶数对.试题解析:(Ⅰ)依题意,
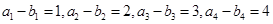 ,相加得,
,相加得,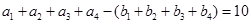 ,又
,又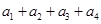
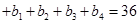 ,
,则
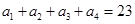 ,
,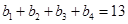 .
.“4项相关数列”
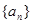 :8,4,6,5;
:8,4,6,5;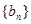 :7,2,3,1(不唯一)3分
:7,2,3,1(不唯一)3分(Ⅱ)不存在.
理由如下:假设存在 “15项相关数列”
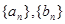 ,
,则
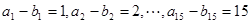 ,相加,得
,相加,得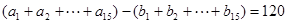
又由已知
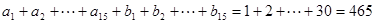 ,由此
,由此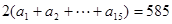 ,显然不可能,所以假设不成立。
,显然不可能,所以假设不成立。从而不存在 “15项相关数列”
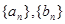 7分
7分(Ⅲ)对于确定的
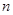 ,任取一对 “
,任取一对 “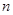 项相关数列”
项相关数列”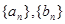 ,
,令
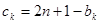 ,
,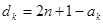
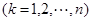 ,
,先证
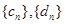 也必为 “
也必为 “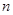 项相关数列” .
项相关数列” .因为
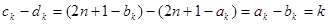
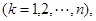
又因为
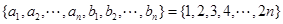 ,很显然有:
,很显然有: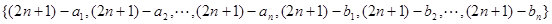
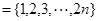
所以
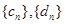 也必为 “
也必为 “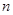 项相关数列”.
项相关数列”.再证数列
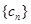 与
与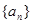 是不同的数列.
是不同的数列.假设
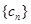 与
与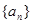 相同,则
相同,则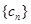 的第二项
的第二项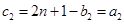 ,又
,又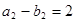 ,则
,则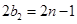 ,即
,即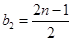 ,显然矛盾.
,显然矛盾.从而,符合条件的“
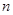 项相关数列”有偶数对. 13分
项相关数列”有偶数对. 13分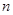 项和公式;2.反证法及其应用
项和公式;2.反证法及其应用
练习册系列答案
相关题目
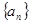 ,
,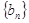 分别为等比,等差数列,数列
分别为等比,等差数列,数列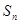 ,且
,且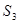 ,
,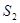 ,
,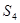 成等差数列,
成等差数列,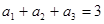 ,数列
,数列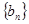 中,
中,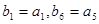 ,
,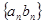 的前n项和为
的前n项和为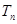 ,求满足不等式
,求满足不等式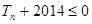 的最小正整数
的最小正整数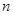 。
。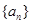 为递增等差数列,且
为递增等差数列,且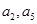 是方程
是方程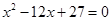 的两根.数列
的两根.数列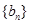 为等比数列,且
为等比数列,且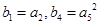 .
.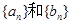 的通项公式;
的通项公式;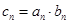 ,求数列
,求数列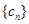 的前
的前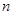 项和
项和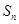 .
.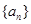 的前
的前 项和为
项和为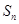 ,若
,若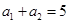 ,
,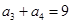 ,则
,则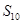 为( )
为( )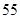
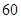
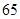
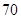
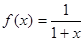 ,各项均为正数的数列
,各项均为正数的数列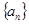 满足
满足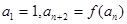 ,若
,若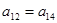 ,则
,则 .
.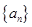 是等差数列,
是等差数列,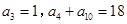 ,则首项
,则首项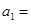 .
.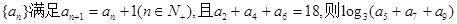 等于( )
等于( )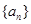 满足
满足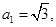
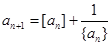
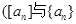 分别表示
分别表示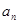 的整数部分与分数部分),则
的整数部分与分数部分),则 .
.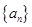 中,若
中,若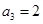 ,则
,则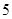 项和
项和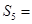 ( )
( )