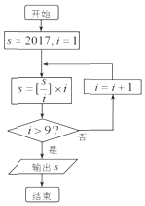
题目内容
【题目】已知函数![]()
(Ⅰ)当![]() 时,
时, ![]() 取得极值,求
取得极值,求![]() 的值;
的值;
(Ⅱ)当函数![]() 有两个极值点
有两个极值点![]() ,且
,且![]() 时,总有
时,总有![]()
![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:⑴求导后,代入![]() ,
, ![]() 取得极值,从而计算出
取得极值,从而计算出![]() 的值,并进行验证(2)由函数
的值,并进行验证(2)由函数![]() 有两个极值点算出
有两个极值点算出![]() ,继而算出
,继而算出![]() ,不等式转化为
,不等式转化为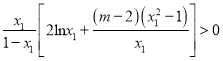 ,构造新函数
,构造新函数![]() ,分类讨论
,分类讨论![]() 、
、![]() 、
、![]() 时三种情况,从而计算出结果
时三种情况,从而计算出结果
解析:(Ⅰ) ![]() ,
, ![]() ,则
,则![]()
检验![]() 时,
时, ![]() ,
,
所以![]() 时,
时, ![]() ,
, ![]() 为增函数;
为增函数;
![]() 时,
时, ![]() ,
, ![]() 为减函数,所以
为减函数,所以![]() 为极大值点
为极大值点
(Ⅱ)![]() 定义域为
定义域为![]() ,有两个极值点
,有两个极值点![]() ,则
,则![]() 在
在![]() 上有两个不等正根
上有两个不等正根
所以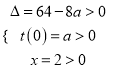 ,所以
,所以![]()
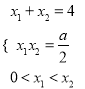 .所以
.所以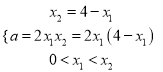 ,所以
,所以![]()
这样原问题即![]() 且
且![]() 时,
时, ![]() 成立
成立
即![]()
即![]()
即![]() ,即
,即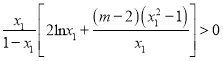
且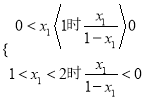
设![]()
![]()
①![]() 时,
时, ![]() ,
,
所以![]() 在
在![]() 上为增函数且
上为增函数且![]() ,
,
所以, ![]() 时,
时, ![]() 不合题意舍去.
不合题意舍去.
②![]() 时,
时, ![]() 同①舍去
同①舍去
③![]() 时
时
(ⅰ)![]() ,即
,即![]() 时可知
时可知![]() ,在
,在![]() 上
上![]() 为减函数且
为减函数且![]() ,
,
这样![]() 时,
时, ![]() ,
, ![]() 时
时![]() ,
,
这样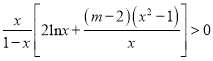 成立
成立
(ⅱ)![]() ,即
,即![]() 时
时![]() 分子中的一元二次函数的对称轴
分子中的一元二次函数的对称轴![]() 开口向下,且1的函数值为
开口向下,且1的函数值为![]()
令![]() ,则
,则![]() 时,
时, ![]() ,
, ![]() 为增函数,
为增函数, ![]()
所以, ![]() 故舍去
故舍去
综上可知: ![]()

练习册系列答案
相关题目
【题目】某学生对其亲属30人的饮食习惯进行了一次调查,并用下图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主)
(1)根据以上数据完成下面的2×2列联表:
主食 蔬菜 | 主食 肉类 | 总计 | |
50岁以下 | |||
50岁以上 | |||
总计 |
(2)能否在犯错误的概率不超过0.010的前提下认为“其亲属的饮食习惯与年龄有关”?并写出简要分析.
附参考公式:![]()
|
|
|
|
|
|
|
|
|
|
|
|