��Ŀ����
ij�صij���۸�涨����aԪ������3���3�����Ժ�ÿ����bԪ���㣬������7�������10���ﰴÿ����cԪ���㣨����a��b��c�涨Ϊ���ij�������c��b�������費���Ƕ³��ͺ��̵Ƶ�������ķ��ã�Ҳ������ʵ����ȡ����ȥ������һԪ����ͷ��ʵ���������ÿһ�γ˳��ij������г����Ψһȷ����
��1����ȡa=14��b=2.4��c=3.6��С���˳����ѧУ���ң���8���������Ӧ������Ѷ���Ԫ������С��ֻ��Ҫ�ش��������
��2����y��Ԫ�����г����x�����֮��ĺ�����ϵʽy=f��x����
��1����ȡa=14��b=2.4��c=3.6��С���˳����ѧУ���ң���8���������Ӧ������Ѷ���Ԫ������С��ֻ��Ҫ�ش��������
��2����y��Ԫ�����г����x�����֮��ĺ�����ϵʽy=f��x����
���㣺�ֶκ�����Ӧ��,����ģ�͵�ѡ����Ӧ��
ר�⣺Ӧ����,���������ʼ�Ӧ��
��������1���������֪����8�����ڵ�ǰ3������շ���14Ԫ������3�����10��������ÿ���ﰴ2.4Ԫ�Ƽۣ���8-3=5������շ���5��2.4=12Ԫ��������Ӽ���С��Ӧ���ij��ѣ�
��2�������������ǰ3�������3�����10�������ڡ�����10����ֱ�д�������ı���ʽ������÷ֶκ�����ʾ��
��2�������������ǰ3�������3�����10�������ڡ�����10����ֱ�д�������ı���ʽ������÷ֶκ�����ʾ��
���
�⣺��1���������֪����3�������ڣ�����14Ԫ������8�����ڵ�ǰ3������շ���14Ԫ������3�����10��������ÿ���ﰴ2.4Ԫ�Ƽۣ���8-3=5������շ���5��2.4=12Ԫ���ܹ��շ�14+12=26��Ԫ��
����Ӧ���������26Ԫ��
��2��3�������ڼ���aԪ����0��x��3ʱ��y=a��Ԫ����
����3�����������10����ʱ����3��x��10ʱ���շ�y=a+��x-3��b=bx+a-3b��Ԫ����
����10����ʱ����x��10ʱ���շ�y=a+7��b+��x-10��c=cx+a+7b-10c��Ԫ����
��y=
��
����Ӧ���������26Ԫ��
��2��3�������ڼ���aԪ����0��x��3ʱ��y=a��Ԫ����
����3�����������10����ʱ����3��x��10ʱ���շ�y=a+��x-3��b=bx+a-3b��Ԫ����
����10����ʱ����x��10ʱ���շ�y=a+7��b+��x-10��c=cx+a+7b-10c��Ԫ����
��y=
|
���������⿼���Ƿֶκ�����Ӧ�ã��ֶ�ģ���ǽ��ʵ������ĺ���Ҫ�ĺ���ģ�ͣ����ص����ڲ�ͬ���Ա���ȡֵ��Χ�ڣ���������ʽ��ͬ��

��ϰ��ϵ�д�
�����Ŀ
��������f��x��=
sinx-
cosx��ͼ������ƽ��m����λ���ȣ��õ���ͼ�����ԭ��Գƣ���m=��������
| ||
| 4 |
| 1 |
| 4 |
A��
| ||
B��
| ||
C��
| ||
D��
|
��֪m��n��������ͬ��ֱ�ߣ����������������غϵ�ƽ�棬������������ȷ���ǣ�������
| A����m��n��n?������mƽ����ƽ����ڵ�����һ��ֱ�� |
| B����m?����m�֣�n�֣������ |
| C����m�ͦ���n�ͦ£�m��n������Φ� |
| D�������Φ£�m?����n?�£���m��n |
��֪��P��x��y����������������
����x2+y2�����ֵΪ��������
|
| A��17 | B��18 | C��20 | D��21 |
��f��x��=lg��4-x2������f��
��+f��
���Ķ������ǣ�������
| x |
| 2 |
| 2 |
| x |
| A����-1��1�� |
| B����-4��4�� |
| C����-4��-1���ȣ�1��4�� |
| D����-2��-1���ȣ�1.2�� |
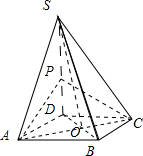 ��ͼ������S-ABCD�У�����ABCD�����Σ���Խ��ߵĽ���ΪO����SA=SC��SA��BD��
��ͼ������S-ABCD�У�����ABCD�����Σ���Խ��ߵĽ���ΪO����SA=SC��SA��BD��